题目内容
设函数,f(x)=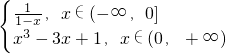 ,若方程f(x)-m=0有且仅有两个实数根,则实数m的取值范围是
,若方程f(x)-m=0有且仅有两个实数根,则实数m的取值范围是
- A.-1<m≤1
- B.-1<m<0或m=1
- C.-1<m≤0或m=1
- D.-1<m≤0
C
分析:由题意可得,函数y=f(x)的图象和直线 y=m有2个交点.利用导数确定函数f(x)的单调性以及值域,数形结合求得实数m的取值范围.
解答:由题意可得,函数y=f(x)的图象和直线 y=m有2个交点.
当x≤0时,f(x)= 是增函数,且 0<f(x)≤1.
是增函数,且 0<f(x)≤1.
当x>0时,f(x)=x3-3x+1,令 f′(x)=3 x2-3=0,可得x=1. 由于 f′(x)在(0,1)上小于0,在(1,+∞)上大于0,
故f(x) 在(0,1)上是减函数,在(1,+∞)上是增函数,故 f(x)的最小值为 f(1)=-1,当x趋于+∞时,f(x)趋于+∞.
如图所示:
故m=1,或-1<m≤0,
故选C.
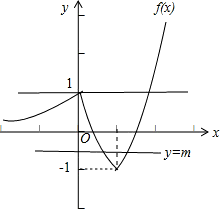
点评:本题主要考查函数的零点的定义,函数的零点与方程的根的关系,体现了转化、数形结合的数学思想,属于中档题.
分析:由题意可得,函数y=f(x)的图象和直线 y=m有2个交点.利用导数确定函数f(x)的单调性以及值域,数形结合求得实数m的取值范围.
解答:由题意可得,函数y=f(x)的图象和直线 y=m有2个交点.
当x≤0时,f(x)=
 是增函数,且 0<f(x)≤1.
是增函数,且 0<f(x)≤1.当x>0时,f(x)=x3-3x+1,令 f′(x)=3 x2-3=0,可得x=1. 由于 f′(x)在(0,1)上小于0,在(1,+∞)上大于0,
故f(x) 在(0,1)上是减函数,在(1,+∞)上是增函数,故 f(x)的最小值为 f(1)=-1,当x趋于+∞时,f(x)趋于+∞.
如图所示:
故m=1,或-1<m≤0,
故选C.
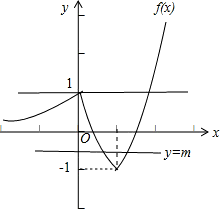
点评:本题主要考查函数的零点的定义,函数的零点与方程的根的关系,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目