题目内容
已知复数 在复平面内所对应的点为
在复平面内所对应的点为 .
.
(1)若复数 为纯虚数,求实数
为纯虚数,求实数 的值;
的值;
(2)若点 在第二象限,求实数
在第二象限,求实数 的取值范围;
的取值范围;
(3)求 的最小值及此时实数
的最小值及此时实数 的值.
的值.
【答案】
(1) (2)
(2) 或
或 (3)
(3) 有最小值
有最小值 .
.
【解析】(1)复数 为纯虚数的条件是
为纯虚数的条件是 .
.
所以先求出z+4m的代数形式.再利用纯虚数的条件建立m的方程求解即可.
(2)复数的实部对应点的横坐标,虚数对应点的纵坐标,根据第三象限点满足条件是a<0,b<0,建立关于m的不等式组,解不等式组即可求解.
(3)根据 建立关于m的函数,根据函数的方法求最值即可
建立关于m的函数,根据函数的方法求最值即可
(1)由 解得
解得 …………………4分
…………………4分
注:未舍解的扣2分
(2)由 …………………6分
…………………6分
解得 或
或 ………………………………………………………8分
………………………………………………………8分
(3) …………………………9分
…………………………9分
令 ,……………………………………………………11分
,……………………………………………………11分
则 …………………………12分
…………………………12分
所以当 即
即 时,…………………………13分
时,…………………………13分
 有最小值
有最小值

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 ,且
,且 ,i为虚数单位,则复数
,i为虚数单位,则复数 在复平面内所对应的点位于( )
在复平面内所对应的点位于( ) 在复平面内的对应点分别为点A、B,则线段AB的中点所对应的复数是
在复平面内的对应点分别为点A、B,则线段AB的中点所对应的复数是 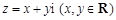 在复平面上对应的点为
在复平面上对应的点为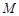 .
.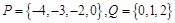 ,从集合
,从集合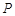 中随机取一个数作为
中随机取一个数作为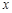 ,从集合
,从集合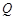 中随机取一个数作为
中随机取一个数作为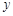 ,求复数
,求复数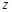 为纯虚数的概率;[来源:.COM][来源:.COM]
为纯虚数的概率;[来源:.COM][来源:.COM]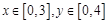 ,求点
,求点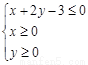 所表示的平面区域内的概率.
所表示的平面区域内的概率.