题目内容
【题目】椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,右顶点为A,上顶点为B,且满足向量
,右顶点为A,上顶点为B,且满足向量![]()
(1)若A![]() ,求椭圆的标准方程;
,求椭圆的标准方程;
(2)设P为椭圆上异于顶点的点,以线段PB为直径的圆经过F1,问是否存在过F2的直线与该圆相切?若存在,求出其斜率;若不存在,说明理由。
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)由题易知![]() ,因为
,因为![]() ,所以
,所以![]() 为等腰三角形
为等腰三角形
所以b=c,由此可求![]() ,即可得到椭圆的标准方程;
,即可得到椭圆的标准方程;
(2)由(1)可得![]() .
.![]() ,P的坐标为
,P的坐标为![]()
则![]() 由题意得
由题意得![]() ,即
,即![]() ,又因为P在椭圆上,所以
,又因为P在椭圆上,所以![]() ,联立可得
,联立可得![]()
设圆心为![]() ,则
,则![]() ,利用两点间的距离公式可得圆的半径r.设直线的方程为:
,利用两点间的距离公式可得圆的半径r.设直线的方程为:![]() .利用直线与圆相切的性质即可得出.
.利用直线与圆相切的性质即可得出.
(1)易知![]() ,因为
,因为![]()
所以![]() 为等腰三角形
为等腰三角形
所以b=c,由![]() 可知
可知![]()
故椭圆的标准方程为:![]()
(2)由已知得![]() ,
,![]()
设椭圆的标准方程为![]() ,P的坐标为
,P的坐标为![]()
因为![]() ,所以
,所以![]()
由题意得![]() ,所以
,所以![]()
又因为P在椭圆上,所以![]() ,由以上两式可得
,由以上两式可得![]()
因为P不是椭圆的顶点,所以![]() ,故
,故![]()
设圆心为![]() ,则
,则![]()
圆的半径![]()
假设存在过![]() 的直线满足题设条件,并设该直线的方程为
的直线满足题设条件,并设该直线的方程为![]()
由相切可知![]() ,所以
,所以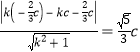
即![]() ,解得
,解得![]()
故存在满足条件的直线。

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
