题目内容
阅读与理解:asinx+bcosx=
sin(x+φ)给出公式:
我们可以根据公式将函数g(x)=sinx+
cosx化为:g(x)=2(
sinx+
cosx)=2(sinxcos
+cosxsin
)=2sin(x+
)
(1)根据你的理解将函数f(x)=
sinx+
cosx化为f(x)=Asin(ωx+φ)的形式.
(2)求出上面函数f(x)的最小正周期、对称中心及单调递增区间.
| a2+b2 |
我们可以根据公式将函数g(x)=sinx+
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
(1)根据你的理解将函数f(x)=
| 3 |
| 2 |
| ||
| 2 |
(2)求出上面函数f(x)的最小正周期、对称中心及单调递增区间.
①由题意f(x)=
sinx+
cosx=
(
sinx+
cosx)=
sin(x+
)
②由①中的解析式知:T=2π,
中心(kπ-
,0),(k∈Z),
令x+
∈[2kπ-
,2kπ+
],k∈z
解得,函数的递增区间[2kπ-
,2kπ+
],(k∈Z)
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| π |
| 6 |
②由①中的解析式知:T=2π,
中心(kπ-
| π |
| 6 |
令x+
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
解得,函数的递增区间[2kπ-
| 2π |
| 3 |
| π |
| 3 |

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
 和角
和角 的终边分别与单位圆交于
的终边分别与单位圆交于 ,
, 两点,(其中
两点,(其中
 ,点
,点 ,求
,求 的值;
的值; , 求
, 求 的值.
的值.
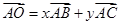 ,且2x+10y=5,则边BC的长
,且2x+10y=5,则边BC的长