Question

（本题满分16分）

如图，公园内有一块边长为2a的正三角形ABC空地，拟改建成花园，并在其中建一直道DE

方便花园管理. 设D、E分别在AB、AC上，且DE均分三角形ABC的面积.

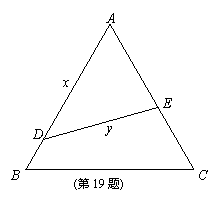（1）设AD=x（），DE=y，试将y表示为x的函数关系式；

（2）若DE是灌溉水管，为节约成本，希望其最短，DE的位置应在哪里？

     若DE是参观路线，希望其最长，DE的位置应在哪里？

Answer 1

【解】（1）因为DE均分三角形ABC的面积，

所以，即.      …………………………2分

在△ADE中，由余弦定理得

.                 …………………………4分

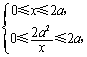因为，所以 解得.

故y关于x的函数关系式为.        …………………………6分

（2）令，则，且.

设.                                …………………………8分

若，则

所以在上是减函数. 同理可得在上是增函数. ………………11分

于是当即时，，此时DE//BC，且 ……………………13分

当或即x=a或2a时，，此时DE为AB或AC上的中线. …………15分

故当取且DE//BC时，DE最短；当D与B重合且E为AC中点，或E与C重合且D为AB中点时，DE最长.                                         …………………………16分

（注：若由，当且仅当即时取“=”号. 只得到最小值，给4分）