题目内容
已知向量 ,
,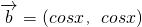 ,若f(x)=
,若f(x)= ,
,
求:(Ⅰ)f(x)的最小正周期及 的值;
的值;
(Ⅱ)f(x)的单调增区间.
解:向量 ,
,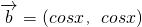 ,
,
f(x)= =cos2x+sinxcosx
=cos2x+sinxcosx
= (1+cos2x)+
(1+cos2x)+ sin2x
sin2x
= sin(2x+
sin(2x+ )+
)+ .
.
(Ⅰ)f(x)的最小正周期为:T= =π,
=π,
 =
= sin(2×
sin(2× +
+ )+
)+ =
= .
.
(Ⅱ)因为2k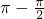 ≤2x+
≤2x+ ,k∈Z,
,k∈Z,
 ,k∈Z,
,k∈Z,
所以f(x)的单调增区间为: ,k∈Z.
,k∈Z.
分析:利用向量的数量积以及二倍角的三角函数结合两角和的正弦函数,化简函数的表达式,
(Ⅰ)利用正弦函数的周期公式直接求解f(x)的最小正周期,直接求解 的值;
的值;
(Ⅱ)利用正弦函数的单调增区间求解函数f(x)的单调增区间.
点评:本题通过向量的数量积,三角函数的二倍角、两角和的三角函数化简函数的表达式,考查函数的基本性质,考查计算能力.
 ,
,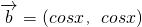 ,
,f(x)=
 =cos2x+sinxcosx
=cos2x+sinxcosx=
 (1+cos2x)+
(1+cos2x)+ sin2x
sin2x=
 sin(2x+
sin(2x+ )+
)+ .
.(Ⅰ)f(x)的最小正周期为:T=
 =π,
=π, =
= sin(2×
sin(2× +
+ )+
)+ =
= .
.(Ⅱ)因为2k
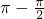 ≤2x+
≤2x+ ,k∈Z,
,k∈Z, ,k∈Z,
,k∈Z,所以f(x)的单调增区间为:
 ,k∈Z.
,k∈Z.分析:利用向量的数量积以及二倍角的三角函数结合两角和的正弦函数,化简函数的表达式,
(Ⅰ)利用正弦函数的周期公式直接求解f(x)的最小正周期,直接求解
 的值;
的值;(Ⅱ)利用正弦函数的单调增区间求解函数f(x)的单调增区间.
点评:本题通过向量的数量积,三角函数的二倍角、两角和的三角函数化简函数的表达式,考查函数的基本性质,考查计算能力.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
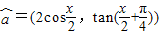 ,
,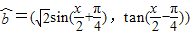 ,令f(x)=
,令f(x)=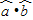
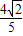 且
且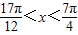 ,求
,求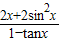 的值.
的值.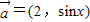 ,
,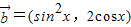 ,函数f(x)=
,函数f(x)=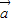 •
•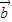 .
.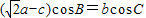 ,求f(A)的取值范围.
,求f(A)的取值范围.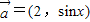 ,
, ,函数f(x)=
,函数f(x)=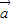 •
•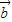 .
.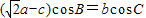 ,求f(A)的取值范围.
,求f(A)的取值范围. ,
, ,若f(x)=
,若f(x)= ,
, 的值;
的值;