题目内容
对任意两个不相等的实数a,b,定义在R上的函数f(x)总有 成立,则必有
成立,则必有
- A.f(a)>f(b)
- B.f(a)<f(b)
- C.f(x)在R上是增函数
- D.f(x)在R上是减函数
D
分析:分析分式的正负,得出函数值随自变量的变化而变化的趋势,从而得出函数的单调性.
解答:因为 ,
,
所以(1)当b-a>0,即b>a时,f(a)-f(b)>0,即f(a)>f(b),所以函数单调递减,
(2)当b-a<0,即b<a时,f(a)-f(b)<0,即f(a)<f(b),所以函数单调递减,
综上,函数在R上单调递减,
故选D.
点评:本题考察函数单调性的判断,是定义形式的变形,属基础题.
分析:分析分式的正负,得出函数值随自变量的变化而变化的趋势,从而得出函数的单调性.
解答:因为
 ,
,所以(1)当b-a>0,即b>a时,f(a)-f(b)>0,即f(a)>f(b),所以函数单调递减,
(2)当b-a<0,即b<a时,f(a)-f(b)<0,即f(a)<f(b),所以函数单调递减,
综上,函数在R上单调递减,
故选D.
点评:本题考察函数单调性的判断,是定义形式的变形,属基础题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
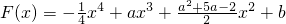 .(a,b为常数)
.(a,b为常数) x4+ax3+
x4+ax3+ x2+b,(a,b为常数),
x2+b,(a,b为常数), .(a,b为常数)
.(a,b为常数) .(a,b为常数)
.(a,b为常数)