��Ŀ����
17��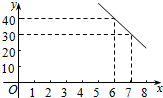 ij��˾����һ�ֳɱ�����Ϊ50Ԫ/�����²�Ʒ���涨����ʱ���۵��۲����ڳɱ����ۣ��ֲ�����80Ԫ/�������������飬����������y�����������۵���x��Ԫ/�����ɽ��ƿ���һ�κ���y=kx+b�Ĺ�ϵ����ͼ��ʾ����
ij��˾����һ�ֳɱ�����Ϊ50Ԫ/�����²�Ʒ���涨����ʱ���۵��۲����ڳɱ����ۣ��ֲ�����80Ԫ/�������������飬����������y�����������۵���x��Ԫ/�����ɽ��ƿ���һ�κ���y=kx+b�Ĺ�ϵ����ͼ��ʾ������1������ͼ����һ�κ���y=kx+b�Ľ���ʽ��
��2���蹫˾��õ�����ΪSԪ������=�����ܼ�-�ɱ��ܼۣ������ܼ�=���۵��ۡ����������ɱ��ܼ�=�ɱ����ۡ�����������
���������۵���x��ʾ����S��
���������۵��۶�Ϊ����ʱ���ù�˾�ɻ�����������������Ƕ��٣���ʱ���������Ƕ��٣�
���� ��1�����ȸ���һ�κ���y=kx+b�ı���ʽ������ֵ����Ȼ�����k��b�����һ�κ�������ʽ��
��2����ͨ����1��ֱ��д��s�ı���ʽ������
�ڸ��ݶ��κ��������ֵ��
��� �⣺��1����ͼ���֪��$\left\{\begin{array}{l}{40=60k+b}\\{30=70k+b}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-1}\\{b=100}\end{array}\right.$��
����y=-x+100��50��x��80����
��2�����ɣ�1��
S=xy-50y
=��-x+100����x-50��
=-x2+150x-5000����50��x��80����
���ɢٿ�֪��S=-��x-75��2+625��
��ͼ�����£��Գ���Ϊx=75��
���Ե�x=75ʱ��Smax=625��
���ù�˾�ɻ�õ����ë����Ϊ625Ԫ��
��ʱ��Ӧ�����۵���Ϊ75Ԫ/����
���� ���⿼�麯��ģ�͵�Ӧ�ã��Լ�һ�κ��������κ�����Ӧ�ã����ڻ����⣮

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
5���ڱ߳�Ϊ2��������ABCD�У���P�ر�BC��CD�����˵㣩��ʱ���˶������BAP=x��AP�ij�Ϊy����ô����y=f��x���Ĵ���ͼ��Ϊ��������
| A�� | 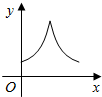 | B�� | 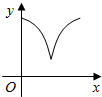 | C�� | 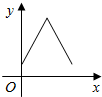 | D�� |  |
8����֪f��2��=-$\frac{4}{3}$��f�䣨2��=-1����$\underset{lim}{x��2}$$\frac{3f��x��+2x}{x-2}$��ֵ�ǣ�������
| A�� | 1 | B�� | 2 | C�� | -1 | D�� | -2 |
5��Բ$��=2sin����+\frac{��}{4}��$��Բ�������ǣ�������
| A�� | $��{1��\frac{��}{4}}��$ | B�� | $��{\frac{1}{2}��\frac{��}{4}}��$ | C�� | $��{\sqrt{2}��\frac{��}{4}}��$ | D�� | $��{2��\frac{��}{4}}��$ |
12���ӳ��ȷֱ�Ϊ2��3��4��5���߶�����ȡ�����������������߶�Ϊ�߿��Թ��������εĸ����ǣ�������
| A�� | $\frac{3}{4}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{2}{3}$ |