Question

对于任意实数x，y定义运算“?”如下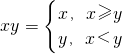：，则函数f（x）=2^x?log ₂（2-x）的值域为________．

Answer 1

[1，+∞）
分析：实数x，y定义运算“?”是求x，y的最大值，分别作出函数y=2^x和y=log ₂（2-x）的图象，结合函数y=2^x和y=log ₂（2-x）的图象可知，在这两个函数的交点处函数f（x）的最大值，从而得出函数的值域．
解答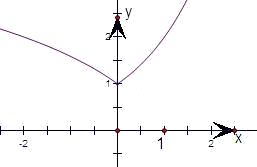：解：分别作出函数y=2^x和y=log ₂（2-x）的图象，
结合函数y=2^x和y=log ₂（2-x）的图象可知，
函数f（x）=2^x?log ₂（2-x）的图象，
在这两个函数的交点处函数y=2^x和y=log ₂（2-x）的最小值．
∴函数f（x）=2^x?log ₂（2-x）的最小值是1．
则函数f（x）=2^x?log ₂（2-x）的值域为[1，+∞）
故答案是[1，+∞）．
点评：本小题主要考查函数单调性的应用、函数的值域、分段函数的解析式求法及其图象的作法等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．数形结合是求解这类问题的有效方法．