题目内容
增函数y=f(x),(x∈R)对任意x,y都有f(x+y)=f(x)+f(y).
(Ⅰ)求f(0)
(Ⅱ)求证f(x)为奇函数;
(Ⅲ)若f(k•3x)+f(3x-9x+3)<0对任意k∈[-1,1]恒成立,求实数x的取值范围.
(Ⅰ)求f(0)
(Ⅱ)求证f(x)为奇函数;
(Ⅲ)若f(k•3x)+f(3x-9x+3)<0对任意k∈[-1,1]恒成立,求实数x的取值范围.
分析:(Ⅰ)根据恒等式,赋值x=y=0,即可求得f(0)的值;
(Ⅱ)根据恒等式,赋值y=-x,即可得f(-x)+f(x)=f(0),再根据(Ⅱ)中的结论,即可得到f(-x)=-f(x),根据奇函数的定义,即可证明结论;
(Ⅲ)根据(Ⅱ)中的结论,函数f(x)为奇函数,将不等式f(k•3x)+f(3x-9x+3)<0转化为f(k•3x)<f(-3x+9x-3),再根据已知条件函数f(x)为R上的增函数,利用单调性去掉“f”,将不等式转化为k•3x<-3x+9x-3对任意k∈[-1,1]成立,构造函数g(k)=32x-(1+k)•3x-3,利用一次函数的性质,即可得到不等式组,求解不等式组,即可得到实数x的取值范围.
(Ⅱ)根据恒等式,赋值y=-x,即可得f(-x)+f(x)=f(0),再根据(Ⅱ)中的结论,即可得到f(-x)=-f(x),根据奇函数的定义,即可证明结论;
(Ⅲ)根据(Ⅱ)中的结论,函数f(x)为奇函数,将不等式f(k•3x)+f(3x-9x+3)<0转化为f(k•3x)<f(-3x+9x-3),再根据已知条件函数f(x)为R上的增函数,利用单调性去掉“f”,将不等式转化为k•3x<-3x+9x-3对任意k∈[-1,1]成立,构造函数g(k)=32x-(1+k)•3x-3,利用一次函数的性质,即可得到不等式组,求解不等式组,即可得到实数x的取值范围.
解答:解:(Ⅰ)令x=y=0,代入f(x+y)=f(x)+f(y),得f(0+0)=f(0)+f(0),
即 f(0)=0;
(Ⅱ)令y=-x,代入f(x+y)=f(x)+f(y),得 f(x-x)=f(x)+f(-x),
又∵f(0)=0,
∴0=f(x)+f(-x),即f(-x)=-f(x)对任意x∈R成立,
∴f(x)是奇函数;
(Ⅲ)∵f(x)在R上是增函数,又由(Ⅱ)知f(x)是奇函数,
∴f(k•3x)<-f(3x-9x+3)=f(-3x+9x-3),
∴k•3x<-3x+9x-3,
即32x-(1+k)•3x-3>0对任意k∈[-1,1]成立,
令g(k)=32x-(1+k)•3x-3,
则
,
即
,
即
,
∴x>1,
∴实数x的取值范围是x>1.
即 f(0)=0;
(Ⅱ)令y=-x,代入f(x+y)=f(x)+f(y),得 f(x-x)=f(x)+f(-x),
又∵f(0)=0,
∴0=f(x)+f(-x),即f(-x)=-f(x)对任意x∈R成立,
∴f(x)是奇函数;
(Ⅲ)∵f(x)在R上是增函数,又由(Ⅱ)知f(x)是奇函数,
∴f(k•3x)<-f(3x-9x+3)=f(-3x+9x-3),
∴k•3x<-3x+9x-3,
即32x-(1+k)•3x-3>0对任意k∈[-1,1]成立,
令g(k)=32x-(1+k)•3x-3,
则
|
即
|
即
|
∴x>1,
∴实数x的取值范围是x>1.
点评:本题考查了抽象函数及其应用,函数单调性的应用和奇偶性的证明,函数的恒成立问题.证明函数的奇偶性要抓住函数奇偶性的定义,函数的恒成立问题一般选用参变量分离法、最值法、数形结合进行求解.属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
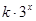 )+f(3
)+f(3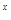 -9
-9