题目内容
(12分)定义在R上的增函数y=f(x)对任意x,y∈R都有f(x+y)=f(x)+f(y).
(Ⅰ)求f(0)
(Ⅱ)求证f(x)为奇函数;
(Ⅲ)若f(解析:(Ⅰ)令x=y=0,代入①式,得f(0+0)=f(0)+f(0),即 f(0)=0.… 2分
(Ⅱ)令y=-x,代入①式,得 f(x-x)=f(x)+f(-x),又f(0)=0,则有
0=f(x)+f(-x).即f(-x)=-f(x)对任意x∈R成立,
所以f(x)是奇函数. ………………………………6分
(Ⅲ) 因为f(x)在R上是增函数,又由(Ⅱ)知f(x)是奇函数.
f(![]() )<-f(3
)<-f(3![]() -9
-9![]() -2)=f(-3
-2)=f(-3![]() +9
+9![]() +2),
+2), ![]() <-3
<-3![]() +9
+9![]() +2,
+2,
3![]() -(1+k)
-(1+k)![]()
![]() +2>0对任意x∈R成立. …… …………………8分
+2>0对任意x∈R成立. …… …………………8分
令t=3![]() >0,问题等价于t
>0,问题等价于t![]() -(1+k)t+2>0对任意t>0恒成立.
-(1+k)t+2>0对任意t>0恒成立.
![]() ,其对称轴为
,其对称轴为![]()
![]() ………………10分
………………10分
 解得:
解得:![]()
综上所述,当![]() 时,
时,
f(![]() )+f(3
)+f(3![]() -9
-9![]() -2)<0对任意x∈R恒成立.…12分
-2)<0对任意x∈R恒成立.…12分
法二:由![]() <-3
<-3![]() +9
+9![]() +2………………8分
+2………………8分
得![]() ……………9分
……………9分
![]() ,即u的最小值为
,即u的最小值为![]() ,………11分
,………11分
要使对x∈R不等式![]() 恒成立,只要使
恒成立,只要使![]() ……12分
……12分

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
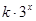 )+f(3
)+f(3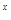 -9
-9