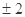题目内容
直线 与圆
与圆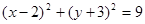 交于
交于 两点,则
两点,则
 (
( 是原点)的面积为
是原点)的面积为
A. | B. | C. | D. |
D
解析试题分析:根据题意,由于直线 与圆
与圆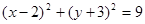 交于
交于 两点,那么圆心(2,-3),半径为3,那么圆心到直线的距离为
两点,那么圆心(2,-3),半径为3,那么圆心到直线的距离为 ,根据半径为3,那么勾股定理可知弦长为
,根据半径为3,那么勾股定理可知弦长为 ,那么原点到直线
,那么原点到直线 的距离为
的距离为

 的面积为
的面积为 ,故答案为D.
,故答案为D.
考点:直线与圆的位置关系
点评:解决的关键是根据圆内的性质来得到弦长和半径以及弦心距的勾股定理来求解,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
过圆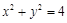 外一点
外一点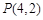 作圆的两条切线,切点分别为
作圆的两条切线,切点分别为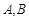 ,则
,则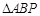 的外接圆方程是( )
的外接圆方程是( )
A.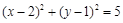 | B.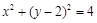 |
C.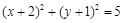 | D.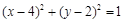 |
直线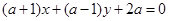 (
(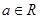 )与圆
)与圆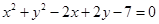 的位置关系是( )
的位置关系是( )
| A.相切 | B.相离 | C.相交 | D.不确定 |
已知直线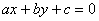 与圆
与圆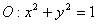 相交于
相交于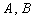 两点,且
两点,且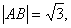 则
则 的值是
的值是
A.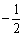 | B.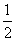 | C.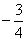 | D.0 |
若圆 上有且只有两个点到直线
上有且只有两个点到直线 的距离为1,则半径
的距离为1,则半径 的取值范围是( )
的取值范围是( )
A.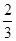 | B. | C. | D.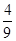 |
直线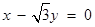 截圆
截圆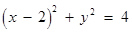 所得劣弧所对的圆心角是
所得劣弧所对的圆心角是
A.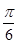 | B.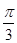 | C.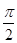 | D.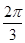 |
以点(-5,4)为圆心,且与 轴相切的圆的方程是( )
轴相切的圆的方程是( )
A. | B. |
C.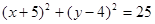 | D. |
已知圆 ,直线
,直线 ,则圆C内任意一点到直线的距离小于
,则圆C内任意一点到直线的距离小于 的概率为( )
的概率为( )
A. | B. | C. | D.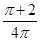 |
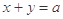 与圆
与圆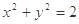 交于A、B两点,O是原点,若
交于A、B两点,O是原点,若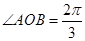 ,则
,则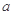 的值为( )
的值为( )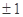 B.
B.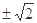 C.
C.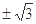 D.
D.