题目内容
(1)已知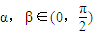 ,且tanα•tanβ<1,比较α+β与
,且tanα•tanβ<1,比较α+β与 的大小;
的大小;(2)试确定一个区间D,
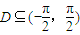 ,对任意的α、β∈D,当
,对任意的α、β∈D,当 时,恒有sinα<cosβ;并说明理由.
时,恒有sinα<cosβ;并说明理由.说明:对于第(2)题,将根据写出区间D所体现的思维层次和对问题探究的完整性,给予不同的评分.
【答案】分析:(1)利用正切化为正弦、余弦,和角公式求出cos(α+β)>0,根据 ,推出α+β与
,推出α+β与 的大小.
的大小.
(2)直接在 内找出一个子区间,区间是固定的,也可以是变化的,对任意的α、β∈D,当
内找出一个子区间,区间是固定的,也可以是变化的,对任意的α、β∈D,当 时,恒有sinα<cosβ,利用函数的单调性,三角函数的符合特征,加以证明即可.
时,恒有sinα<cosβ,利用函数的单调性,三角函数的符合特征,加以证明即可.
解答:解:(1)∵
∴ (2分)=>cos(α+β)>0(2分)
(2分)=>cos(α+β)>0(2分)
∵α+β∈(0,π)
∴ (2分)
(2分)
(2)第一类解答:(1)若取 或取
或取 等固定区间且D是
等固定区间且D是 的子集并说明理由者给(2分),
的子集并说明理由者给(2分),
(2)若取D=[γ1,γ2], ,并说明理由者给(3分)
,并说明理由者给(3分)
理由:
若取 ,
, ,
,
则-1<sinα<0,0<cosβ<1,即sinα<cosβ;
第二类解答:(1)若取 或取
或取 等固定区间且D是
等固定区间且D是 的子集,且解答完整得(4分)
的子集,且解答完整得(4分)
(2)若取D是 的子集且区间的一端是变动者.且解答完整得(5分)
的子集且区间的一端是变动者.且解答完整得(5分)
(3)若取D=[γ1,γ2], ,且解答完整得(6分)
,且解答完整得(6分)
取D=[γ1,γ2],
证明如下,设α,β∈[γ1,γ2], ,
,
又 ,
,
则 ,
,
因为-γ2≤-β≤γ1, ,
,
而 ,
, ,
,
即: ,于是由α,β∈[γ1,γ2],
,于是由α,β∈[γ1,γ2], ,且
,且
以及正弦函数的单调性得: ,即:0<sinα<cosβ
,即:0<sinα<cosβ
第三类解答:
(1)若取 或取
或取 等固定区间且D是
等固定区间且D是 的子集(两端需异号),且解答完整得(6分)
的子集(两端需异号),且解答完整得(6分)
(2)若取D是 的子集且区间的一端是变动者(两端需异号).且解答完整得(7分)
的子集且区间的一端是变动者(两端需异号).且解答完整得(7分)
(3)若取取D=[γ1,γ2], ,(γ1与γ2需异号)且解答完整得(8分)
,(γ1与γ2需异号)且解答完整得(8分)
若取 ,
,
因为: ,
, ,
,
则
亦有: ,
,
这时, ,
, ,
,
而 为
为 ,
,
所以有sinα<cosβ.
(如出现其它合理情况,可斟酌情形给分,但最高不超过8分).
点评:本题考查比较大小,正弦函数的单调性,考查分析问题解决问题的能力,是中档题.
 ,推出α+β与
,推出α+β与 的大小.
的大小.(2)直接在
 内找出一个子区间,区间是固定的,也可以是变化的,对任意的α、β∈D,当
内找出一个子区间,区间是固定的,也可以是变化的,对任意的α、β∈D,当 时,恒有sinα<cosβ,利用函数的单调性,三角函数的符合特征,加以证明即可.
时,恒有sinα<cosβ,利用函数的单调性,三角函数的符合特征,加以证明即可.解答:解:(1)∵

∴
 (2分)=>cos(α+β)>0(2分)
(2分)=>cos(α+β)>0(2分)∵α+β∈(0,π)
∴
 (2分)
(2分)(2)第一类解答:(1)若取
 或取
或取 等固定区间且D是
等固定区间且D是 的子集并说明理由者给(2分),
的子集并说明理由者给(2分),(2)若取D=[γ1,γ2],
 ,并说明理由者给(3分)
,并说明理由者给(3分)理由:
若取
 ,
, ,
,则-1<sinα<0,0<cosβ<1,即sinα<cosβ;
第二类解答:(1)若取
 或取
或取 等固定区间且D是
等固定区间且D是 的子集,且解答完整得(4分)
的子集,且解答完整得(4分)(2)若取D是
 的子集且区间的一端是变动者.且解答完整得(5分)
的子集且区间的一端是变动者.且解答完整得(5分)(3)若取D=[γ1,γ2],
 ,且解答完整得(6分)
,且解答完整得(6分)取D=[γ1,γ2],

证明如下,设α,β∈[γ1,γ2],
 ,
,又
 ,
,则
 ,
,因为-γ2≤-β≤γ1,
 ,
,而
 ,
, ,
,即:
 ,于是由α,β∈[γ1,γ2],
,于是由α,β∈[γ1,γ2], ,且
,且
以及正弦函数的单调性得:
 ,即:0<sinα<cosβ
,即:0<sinα<cosβ第三类解答:
(1)若取
 或取
或取 等固定区间且D是
等固定区间且D是 的子集(两端需异号),且解答完整得(6分)
的子集(两端需异号),且解答完整得(6分)(2)若取D是
 的子集且区间的一端是变动者(两端需异号).且解答完整得(7分)
的子集且区间的一端是变动者(两端需异号).且解答完整得(7分)(3)若取取D=[γ1,γ2],
 ,(γ1与γ2需异号)且解答完整得(8分)
,(γ1与γ2需异号)且解答完整得(8分)若取
 ,
,因为:
 ,
, ,
,则

亦有:
 ,
,这时,
 ,
, ,
,而
 为
为 ,
,所以有sinα<cosβ.
(如出现其它合理情况,可斟酌情形给分,但最高不超过8分).
点评:本题考查比较大小,正弦函数的单调性,考查分析问题解决问题的能力,是中档题.

练习册系列答案
相关题目
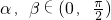 ,且tanα,tanβ是方程x2-5x+6=0的两根.
,且tanα,tanβ是方程x2-5x+6=0的两根.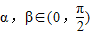 ,且tanα,tanβ是方程x2-5x+6=0的两根.
,且tanα,tanβ是方程x2-5x+6=0的两根. ,且tanα•tanβ<1,比较α+β与
,且tanα•tanβ<1,比较α+β与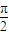 的大小;
的大小; ,对任意的α、β∈D,当
,对任意的α、β∈D,当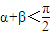 时,恒有sinα<cosβ;并说明理由.
时,恒有sinα<cosβ;并说明理由.