题目内容
已知函数 (a∈R)
(a∈R)(1)若f(1)=1,求实数a的值并计算f(-1)+f(3)的值;
(2)若不等式f(x)≥0对任意的x∈[1,+∞)恒成立,求实数a的取值范围;
(3)当a=-1时,设g(x)=f(x+b),是否存在实数b使g(x)为奇函数.若存在,求出b的值;若不存在,说明理由.
【答案】分析:(1)由f(1)=1,知1+a=1,由此能求出实数a的值和f(-1)+f(3)的值.
(2)由f(x)≥0,知 对任意的x∈[1,+∞)恒成立,构构造函数
对任意的x∈[1,+∞)恒成立,构构造函数 ,能求出实数a的取值范围.
,能求出实数a的取值范围.
(3)由a=-1,知 ,由此能推导出存在b=1,使g(x)是奇函数.
,由此能推导出存在b=1,使g(x)是奇函数.
解答:(本题12分)
解:(1)∵f(1)=1,
∴ ,即1+a=1,∴a=0
,即1+a=1,∴a=0
∴ ,
,
∴ .
.
(2)∵f(x)≥0,即 ,
,
亦即 对任意的x∈[1,+∞)恒成立,
对任意的x∈[1,+∞)恒成立,
设 ,
,
∵ ,
,
∴h(x)在x∈[1,+∞)时是增函数,所以hmin(x)=h(1)=-1
∴a≥-1即可.
故实数a的取值范围是[-1,+∞).
(3)∵a=-1,
∴ ,
,
∴ ,
,
方法一:
∵g(x)是奇函数,且x∈R,∴g(0)=0
∴ ,∴2b-1=21-b,即2b-1=1,所以b=1.
,∴2b-1=21-b,即2b-1=1,所以b=1.
当b=1时, ,∵
,∵ ,
,
∴g(x)是奇函数.
故存在b=1,使g(x)是奇函数.
方法二:
∵g(x)是奇函数,∴g(-x)=-g(x),令b-1=c
即
∴22c+2-2x-22x-2-2c=-(22c+22x-2-2x-2-2c)
∴22c-2-2c=0,即24c=1,即c=0,即b=1.
方法三:【这种做法也给分】
当b=1时, ,
,
∵ ,∴g(x)是奇函数.
,∴g(x)是奇函数.
所以存在b=1,使g(x)是奇函数.
点评:本题考查函数值的求法,考查满足条件的实数的取值范围的求法,探索使得函数为奇函数的实数值是否存在.解题时要认真审题,注意等价转化思想的合理运用.
(2)由f(x)≥0,知
 对任意的x∈[1,+∞)恒成立,构构造函数
对任意的x∈[1,+∞)恒成立,构构造函数 ,能求出实数a的取值范围.
,能求出实数a的取值范围.(3)由a=-1,知
 ,由此能推导出存在b=1,使g(x)是奇函数.
,由此能推导出存在b=1,使g(x)是奇函数.解答:(本题12分)
解:(1)∵f(1)=1,
∴
 ,即1+a=1,∴a=0
,即1+a=1,∴a=0∴
 ,
,∴
 .
.(2)∵f(x)≥0,即
 ,
,亦即
 对任意的x∈[1,+∞)恒成立,
对任意的x∈[1,+∞)恒成立,设
 ,
,∵
 ,
,∴h(x)在x∈[1,+∞)时是增函数,所以hmin(x)=h(1)=-1
∴a≥-1即可.
故实数a的取值范围是[-1,+∞).
(3)∵a=-1,
∴
 ,
,∴
 ,
,方法一:
∵g(x)是奇函数,且x∈R,∴g(0)=0
∴
 ,∴2b-1=21-b,即2b-1=1,所以b=1.
,∴2b-1=21-b,即2b-1=1,所以b=1.当b=1时,
 ,∵
,∵ ,
,∴g(x)是奇函数.
故存在b=1,使g(x)是奇函数.
方法二:
∵g(x)是奇函数,∴g(-x)=-g(x),令b-1=c
即

∴22c+2-2x-22x-2-2c=-(22c+22x-2-2x-2-2c)
∴22c-2-2c=0,即24c=1,即c=0,即b=1.
方法三:【这种做法也给分】
当b=1时,
 ,
,∵
 ,∴g(x)是奇函数.
,∴g(x)是奇函数.所以存在b=1,使g(x)是奇函数.
点评:本题考查函数值的求法,考查满足条件的实数的取值范围的求法,探索使得函数为奇函数的实数值是否存在.解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
相关题目
 (a∈R且a≠0).
(a∈R且a≠0).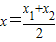 ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. ,a∈R.
,a∈R. 上的任意一个x,都有f(x)≤1成立,求a的取值范围.
上的任意一个x,都有f(x)≤1成立,求a的取值范围. (a∈R).
(a∈R). 在[1,e]上是增函数,求a的取值范围;
在[1,e]上是增函数,求a的取值范围;
 .
.