题目内容
M={(x，y)
|
|
分析：先根据约束条件画出可行域，设z=2x+y，再利用z的几何意义求最值，只需求出何时目标函数z=2x+y在线性约束条（x，y）∈M∪N 下取得最大值时，从而得到实数t的取值范围即可．
解答：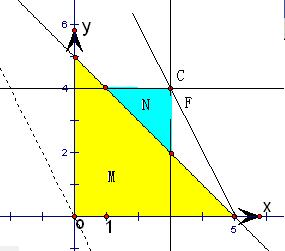
解：如图，M、N表示的区域如图所示，
显然最优解在C处取得，
过点（5，0）作斜率为-2的直线交直线BC：x=3于F，
则C应在点F上方，可求得F（3，4），
∴t＞4．
故答案为：t＞4．
解：如图，M、N表示的区域如图所示，显然最优解在C处取得，
过点（5，0）作斜率为-2的直线交直线BC：x=3于F，
则C应在点F上方，可求得F（3，4），
∴t＞4．
故答案为：t＞4．
点评：本题主要考查了用平面区域二元一次不等式组，以及简单的转化思想和数形结合的思想，属中档题．借助于平面区域特性，用几何方法处理代数问题，体现了数形结合思想、化归思想．线性规划中的最优解，通常是利用平移直线法确定．
练习册系列答案
习题精选系列答案
相关题目
集合M={(x，y)|y=
}，N={（x，y）|x=1，y∈R}，则M∩N等于（ ）
| 1-x2 |
| A、{（1，0）} |
| B、{y|0≤y≤1} |
| C、{1，0} |
| D、∅ |
已知集合M={(x，y)|y=x+m}，N={(x，y)|
，θ∈[-
，
]，若M∩N≠?，则实数m的取值范围是（ ）
|
| π |
| 2 |
| π |
| 2 |
A、(-
| ||||
B、[-
| ||||
C、(-
| ||||
D、[1，
|
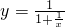的定义域为M，值域为N，那么