题目内容
已知f（x）=|log3x|．（Ⅰ）画出函数f（x）的图象；
（Ⅱ）讨论关于x的方程|log3x|=a（a∈R）的解的个数．
【答案】分析：（Ⅰ）根据对数函数的图象和性质，画出函数f（x）的图象；
（Ⅱ）设函数y=|log3x|和y=a，根据图象之间的关系判断方程解的个数．
解答：解：（Ⅰ）函数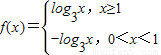
，对应的函数f（x）的图象为：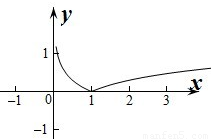
（Ⅱ）设函数y=|log3x|和y=a，
当a＜0时，两图象无交点，原方程解的个数为0个．
当a=0时，两图象只有1个交点，解原方程只有1解．
当a＞0时，两图象有2个交点，即原方程有2解．
点评：本题主要考查对数函数的图象和性质，以及两函数的交点问题，利用数形结合是解决本题的关键．
（Ⅱ）设函数y=|log3x|和y=a，根据图象之间的关系判断方程解的个数．
解答：解：（Ⅰ）函数
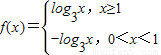，对应的函数f（x）的图象为：（Ⅱ）设函数y=|log3x|和y=a，
当a＜0时，两图象无交点，原方程解的个数为0个．
当a=0时，两图象只有1个交点，解原方程只有1解．
当a＞0时，两图象有2个交点，即原方程有2解．
点评：本题主要考查对数函数的图象和性质，以及两函数的交点问题，利用数形结合是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
(a>0
(a>0
)＋4sin(x＋
)－a，把函数y＝g(x)的图象按向量
(－
，1)平移后得到y＝f(x)的图象．
[f(x)＋8＋a]的值域；
，
]时f(x)＝0恒有解，求实数a的取值范围．
[3-（x-1）2]，求f（x）的值域及单调区间．
[3-（x-1）2]，求f（x）的值域及单调区间．