题目内容
已知函数
，其中
.
（1）若
，求
的值；
（2）证明：当且仅当
时，函数
在区间
上为单调函数；
（3）若函数在区间
上是增函数，求的取值范围．
（1）
（2）证明略 （3）
解析:
（1）由
，可得：
， …………4分
（2）任取
=
=
……………6分
因为
，
，所以
…8分
若
，则
，
在
单调递减 ………………10分
若函数在
为单调函数，则要使得
对于一切满足
条件的
、
恒为正或恒为负，又
，所以必须恒为负，所以 ………12分
综上所述，当且仅当时，函数在为单调减函数．
（3）任取
，
，因为单调递增，
所以
，又
，那么
恒成立 14分
， 所以 ………16分
练习册系列答案
相关题目
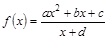（其中a>0），且
在点（0，0）处的切线与直线
平行。
的两个极值点，且
的取值范围；
，其中
为实数，且
在
处取得的极值为
。
的表达式；
处的切线方程。
（其中
是实数常数，
）
，函数
的图像关于点（—1，3）成中心对称，求
的值；
，总有
，求
的取值范围；
，
，且对任意
时，不等式
恒成立，求负实数
的取值范围．
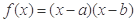（其中
）的图象如图（上）所示，则函数
的图象是（ ） 
