题目内容
【题目】已知平行四边形![]() 中
中![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,三角形
,三角形![]() 为等边三角形,
为等边三角形,![]() .
.
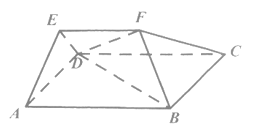
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 平面
平面![]()
①求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
②求二面角![]() 的正弦值.
的正弦值.
【答案】(Ⅰ)见解析;(Ⅱ)①![]() ;②
;②![]() .
.
【解析】
(Ⅰ)先证明![]() ,以
,以![]() 为原点,
为原点,![]() 为
为![]() 轴建立空间直角坐标系,利用向量的数量积为零可得
轴建立空间直角坐标系,利用向量的数量积为零可得![]() ,
,![]() ,从而
,从而![]() 平面
平面![]() ,再由面面垂直的判定定理可得结果;(Ⅱ)设
,再由面面垂直的判定定理可得结果;(Ⅱ)设![]() ,利用
,利用![]() ,求得
,求得![]() ,①求出
,①求出![]() ,
,![]() 的坐标,利用空间向量夹角余弦公式可得结果;②利用向量垂直数量积为零列方程,分别求出平面
的坐标,利用空间向量夹角余弦公式可得结果;②利用向量垂直数量积为零列方程,分别求出平面![]() 的法向量与平面
的法向量与平面![]() 的法向量,由空间向量夹角余弦公式求得二面角的余弦值,进而可得结果.
的法向量,由空间向量夹角余弦公式求得二面角的余弦值,进而可得结果.
(Ⅰ)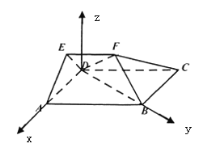
平行四边形![]() 中
中
∵![]() ,
,![]() ,
,
由余弦定理可得![]() ,
,
由勾股定理可得![]() ,
,
如图,以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]()
∴![]() ,
,,
![]() ,
,![]() ,
,![]()
∴![]() ,
,![]() ,
,![]()
∴![]() ,
,![]() ,∴
,∴![]() ,
,![]() .
.
又![]() ,∴
,∴![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(Ⅱ)∵![]() ,∴设
,∴设![]()
∴![]() ,
,![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∴![]() .
.
①![]() ,
,![]()
∴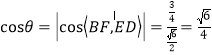
∴异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
②设![]() 为平面
为平面![]() 的法向量,则
的法向量,则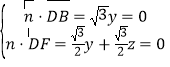
可得![]() ,
,
设![]() 为平面
为平面![]() 的法向量,则
的法向量,则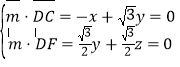
可得![]() ,
,
∴![]() ,
,![]()
∴二面角![]() 的正弦值为
的正弦值为![]() .
.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案【题目】研学旅行是研究性学习和旅行体验相结合的校外教育活动,继承和发展了我国传统游学、“读万卷书,行万里路”的教育理念和人文精神,成为素质教育的新内容和新方式,提升中小学生的自理能力、创新精神和实战能力,是综合实战育人的有效途径,为了了解某校高二年级600名学生在一次研学旅行活动中的武术表演情况,研究人员在该校高二学生中随机抽取了10名学生的武术表演成绩进行统计,统计结果如图所示(满分100分),已知这10名学生或武术表演的平均成绩为85分.
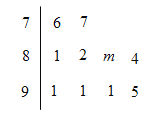
(1)求m的值;
(2)为了研究高二男、女生的武术表演情况,现对该校高二所有学生的武术表演成绩进行分类统计,得到的数据如下表所示:
男生 | 女生 | 合计 | |
武术表演成绩超过80分 | 150 | ||
武术表演成绩不超过80分 | 100 | ||
合计 |
已知随机抽取这600名学生中的一名学生,抽到武术表演成绩超过80分的学生概率是![]() ,根据已知条件完成上面
,根据已知条件完成上面![]() 列联表,并据此判断是否有
列联表,并据此判断是否有![]() 的把握认为武术表演成绩超过80分与性别具有相关性.
的把握认为武术表演成绩超过80分与性别具有相关性.
参考公式: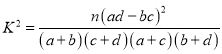 ,其中
,其中![]() .
.
临界值表:
P( | 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |