题目内容
求以(1,-1)为中点的抛物线y2=8x的弦所在直线的方程.
分析:要求过(1,-1)的弦所在的直线方程,只需求出斜率即可.
解:设弦的两端点分别为A(x1,y1),B(x2,y2),则

由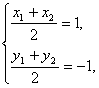 得
得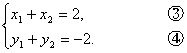
kAB=![]() ,⑤
,⑤
由②-①,得(y2+y1)(y2-y1)=8(x2-x1),
∴![]() =
=![]() .将④⑤代入上式可得kAB=-4.
.将④⑤代入上式可得kAB=-4.
∴弦所在直线方程为y+1=-4(x-1),即4x+y-3=0.

练习册系列答案
相关题目
题目内容
求以(1,-1)为中点的抛物线y2=8x的弦所在直线的方程.
分析:要求过(1,-1)的弦所在的直线方程,只需求出斜率即可.
解:设弦的两端点分别为A(x1,y1),B(x2,y2),则

由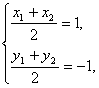 得
得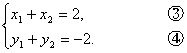
kAB=![]() ,⑤
,⑤
由②-①,得(y2+y1)(y2-y1)=8(x2-x1),
∴![]() =
=![]() .将④⑤代入上式可得kAB=-4.
.将④⑤代入上式可得kAB=-4.
∴弦所在直线方程为y+1=-4(x-1),即4x+y-3=0.
