Question

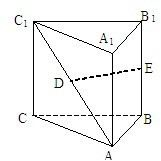如图，在直三棱柱ABC-A₁B₁C₁中，AB=1，AC=2，BC=

3

，D，E分别是AC₁和BB₁的中点，则直线DE与平面BB₁C₁C所成的角为（　　）

• A、

  π

  6

• B、

  π

  4

• C、

  π

  3

• D、

  π

  2

Answer 1

分析：根据题意得ED∥BF，进而得到直线DE与平面BB₁C₁C所成的角等于直线BF与平面BB₁C₁C所成的角．利用几何体的结构特征得到∠FBG=

π

6

．即可得到答案．

解答：解：取AC的中点为F，连接BF、DF．
因为在直三棱柱ABC-A₁B₁C₁中，CC₁∥BB₁，又因为DF是三角形ACC₁的中位线，故DF=

1

2

CC₁=

1

2

BB₁=BE，故四边形BEDF是平行四边形，所以ED∥BF．

过点F作FG垂直与BC交BC与点G，由题意得∠FBG即为所求的角．
因为AB=1，AC=2，BC=

3

，所以∠ABC=

π

2

，∠BCA=

π

6

，直角三角形斜边中线BF是斜边AC的一半，故BF=

1

2

AC=CF，所以
∠FBG=∠BCA=

π

6

．
故选A．

点评：解决此类问题的关键是熟悉线面角的作法，即由线上的一点作平面的垂线再连接斜足与垂足则得到线面角．