题目内容
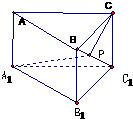 如图,在直三棱柱ABC-A1B1C1中,底面为直角三角形,∠ACB=90°,AC=4,BC=CC1=
如图,在直三棱柱ABC-A1B1C1中,底面为直角三角形,∠ACB=90°,AC=4,BC=CC1=| 2 |
分析:连A1B,沿BC1将△CBC1展开与△A1BC1在同一个平面内,不难看出CP+PA1的最小值是A1C的连线.(在BC1上取一点与A1C构成三角形,因为三角形两边和大于第三边)由余弦定理即可求解.
解答:解:连A1B,沿BC1将△CBC1展开与△A1BC1在同一个平面内,
连接A1C,长度即是所求.
∵直三棱柱ABC-A1B1C1中,底面为直角三角形,∠ACB=90°,AC=4,BC=CC1=
,
∴矩形BCC1B1是边长为
的正方形;则BC1=2;
另外A1C1=AC=4;
在矩形ABB1A1中,A1B1=AB=3
,BB1=
,则A1B=2
;
易发现42+22=20,即A1C12+BC12=A1B2,
∴∠A1C1B=90°,则∠A1C1C=135°
故A1C=
=
=
故答案为:
连接A1C,长度即是所求.
∵直三棱柱ABC-A1B1C1中,底面为直角三角形,∠ACB=90°,AC=4,BC=CC1=
| 2 |
∴矩形BCC1B1是边长为
| 2 |
另外A1C1=AC=4;
在矩形ABB1A1中,A1B1=AB=3
| 2 |
| 2 |
| 5 |
易发现42+22=20,即A1C12+BC12=A1B2,
∴∠A1C1B=90°,则∠A1C1C=135°
故A1C=
|
16+2+2×4•
|
| 26 |
故答案为:
| 26 |
点评:本题考查的知识中是棱柱的结构特征及两点之间的距离,其中利用旋转的思想,将△CBC1沿BC1展开,将一个空间问题转化为平面内求两点之间距离问题是解答本题的关键.

练习册系列答案
相关题目




