题目内容
已知抛物线y2=-x与直线y=k(x+1)相交于A、B两点.(1)求证:OA⊥OB;
(2)当△OAB的面积等于![]() 时,求k的值.
时,求k的值.
(1)证明:如右图,由方程组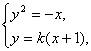 消去x后,整理得ky2+y-k=0.
消去x后,整理得ky2+y-k=0.
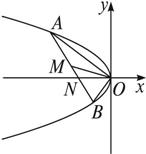
设A(x1,y1)、B(x2,y2),由韦达定理y1·y2=-1.
∵A、B在抛物线y2=-x上,
∴y12=-x1,y22=-x2,y12·y22=x1x2.
∵kOA·kOB=![]() ·
·![]() =
=![]() =
=![]() =-1,
=-1,
∴OA⊥OB.
(2)解:设直线与x轴交于N,又显然k≠0,
∴令y=0,则x=-1,即N(-1,0).
∵S△OAB=S△OAN+S△OBN=![]() |ON||y1|+
|ON||y1|+![]() |ON||y2|=
|ON||y2|=![]() |ON|·|y1-y2|,
|ON|·|y1-y2|,
∴S△OAB=![]() ·1·
·1·![]() =
=![]()
![]() .
.
∵S△OAB=![]() ,∴
,∴![]() =
=![]()
![]() .解得k=±
.解得k=±![]() .
.
点评:联立直线方程与圆锥曲线方程,利用韦达定理化简是本部分的基本方法.

练习册系列答案
相关题目
 (2012•西城区一模)如图,已知抛物线y2=x及两点A1(0,y1)和A2(0,y2),其中y1>y2>0.过A1,A2分别作y轴的垂线,交抛物线于B1,B2两点,直线B1B2与y轴交于点A3(0,y3),此时就称A1,A2确定了A3.依此类推,可由A2,A3确定A4,….记An(0,yn),n=1,2,3,….
(2012•西城区一模)如图,已知抛物线y2=x及两点A1(0,y1)和A2(0,y2),其中y1>y2>0.过A1,A2分别作y轴的垂线,交抛物线于B1,B2两点,直线B1B2与y轴交于点A3(0,y3),此时就称A1,A2确定了A3.依此类推,可由A2,A3确定A4,….记An(0,yn),n=1,2,3,….