题目内容
(本小题满分12分)
已知A、B、C是直线l上的三点,O是直线l外一点,向量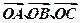 满足
满足
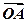 =[f(x
=[f(x )+2f′(1)]
)+2f′(1)]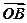 -ln(x+1)
-ln(x+1)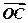 。
。
(Ⅰ)求函数y=f(x)的表达式; (Ⅱ)若x>0,证明:f(x)>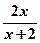 ;
;
(Ⅲ)若不等式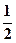 x2≤f(x2)+m2-2m-3对x∈[-1,1]恒成立,求实数m的取值范围。
x2≤f(x2)+m2-2m-3对x∈[-1,1]恒成立,求实数m的取值范围。
已知A、B、C是直线l上的三点,O是直线l外一点,向量
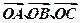 满足
满足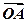 =[f(x
=[f(x )+2f′(1)]
)+2f′(1)]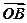 -ln(x+1)
-ln(x+1)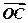 。
。(Ⅰ)求函数y=f(x)的表达式; (Ⅱ)若x>0,证明:f(x)>
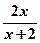 ;
;(Ⅲ)若不等式
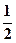 x2≤f(x2)+m2-2m-3对x∈[-1,1]恒成立,求实数m的取值范围。
x2≤f(x2)+m2-2m-3对x∈[-1,1]恒成立,求实数m的取值范围。(1)
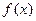 =
=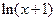
(2)略
(3)
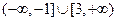
解:(Ⅰ)∵OA=[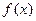 +2
+2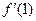 ]OB-
]OB-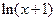 OC,且A、B、C在直线
OC,且A、B、C在直线 上,
上,
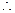
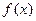 +2
+2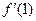 ―
―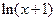 =1,
=1,  …………2分
…………2分
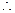 y=
y=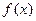 =
=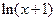 +1-2
+1-2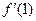 ,
,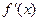 =
=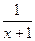 ,网于是
,网于是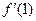 =
=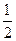 ,
,
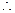
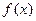 =
=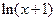 ………4分
………4分
(Ⅱ)令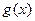 =
=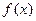 -
-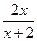 ,由
,由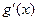 =
=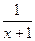 -
-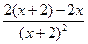 =
=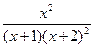 ,
,
以及x>0, 知
知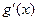 >0,
>0,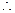
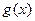 在
在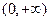 上为增函数,又
上为增函数,又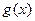 在x=0处右连续,
在x=0处右连续,
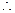 当x>0时,得
当x>0时,得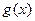 >
>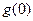 =0,
=0,
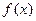 >
>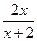 …………8分
…………8分
(Ⅲ)原不等式等价网于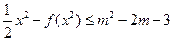 ,
,
令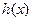 =
=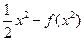 =
=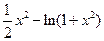 ,则
,则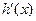 =
=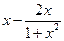 =
=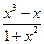 ,…10分
,…10分
∵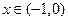 时,
时,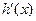 >0,
>0,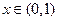 时,
时,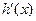 <0,
<0,
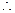
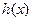 在
在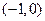 为增函数,在
为增函数,在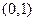 上为减函数, …………11分
上为减函数, …………11分
 当
当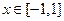 时,
时,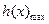 =
=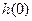 =0,从而依题意有0
=0,从而依题意有0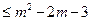 ,
,
解得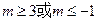 ,故m的取值范围是
,故m的取值范围是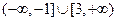 …………12分
…………12分
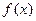 +2
+2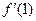 ]OB-
]OB-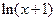 OC,且A、B、C在直线
OC,且A、B、C在直线 上,
上,
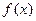 +2
+2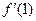 ―
―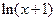 =1,
=1,  …………2分
…………2分 y=
y=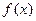 =
=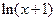 +1-2
+1-2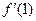 ,
,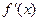 =
=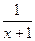 ,网于是
,网于是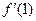 =
=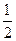 ,
,
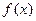 =
=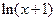 ………4分
………4分(Ⅱ)令
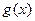 =
=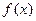 -
-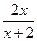 ,由
,由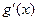 =
=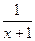 -
-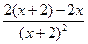 =
=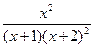 ,
,以及x>0,
 知
知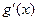 >0,
>0,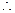
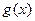 在
在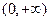 上为增函数,又
上为增函数,又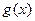 在x=0处右连续,
在x=0处右连续,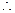 当x>0时,得
当x>0时,得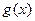 >
>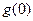 =0,
=0,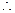
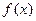 >
>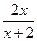 …………8分
…………8分(Ⅲ)原不等式等价网于
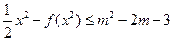 ,
,令
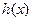 =
=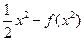 =
=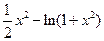 ,则
,则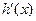 =
=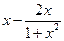 =
=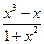 ,…10分
,…10分∵
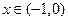 时,
时,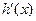 >0,
>0,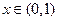 时,
时,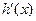 <0,
<0,
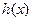 在
在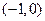 为增函数,在
为增函数,在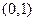 上为减函数, …………11分
上为减函数, …………11分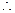 当
当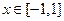 时,
时,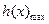 =
=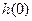 =0,从而依题意有0
=0,从而依题意有0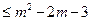 ,
,解得
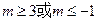 ,故m的取值范围是
,故m的取值范围是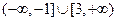 …………12分
…………12分
练习册系列答案
相关题目
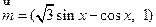 ,
,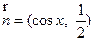 ,若
,若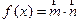 .
.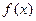 的最小正周期;
的最小正周期;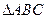 的三内角
的三内角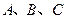 的对边分别为
的对边分别为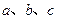 ,且
,且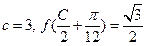
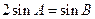 ,求C、
,求C、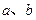 的值.
的值.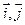 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设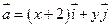 ,
, 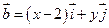 且满足
且满足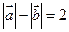
 (x,y)的轨迹E的方程.
(x,y)的轨迹E的方程.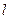 过点
过点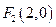 且法向量为
且法向量为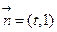 ,直线与轨迹E交于
,直线与轨迹E交于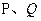 两点.点
两点.点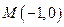 ,无论直线
,无论直线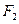 怎样转动,
怎样转动, 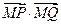 是否为定值?如果是,求出定值;如果不是,请说明理由.并求实数
是否为定值?如果是,求出定值;如果不是,请说明理由.并求实数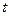 的取值范围;
的取值范围;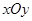 中,
中,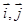 分别是与
分别是与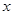 轴、
轴、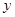 轴正方向同向的单位向量,在直角三角形
轴正方向同向的单位向量,在直角三角形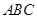 中,若
中,若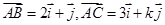 ,则
,则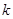 的可能值个数是( )
的可能值个数是( )
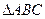 斜边BC的中线,用解析法证明
斜边BC的中线,用解析法证明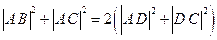 .
.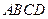 的棱长为1,空间中动点P满足
的棱长为1,空间中动点P满足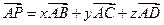
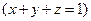 ,则
,则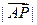 的最小值为…………………………………………………………………………………………( )
的最小值为…………………………………………………………………………………………( )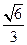
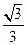
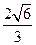
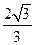
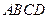 中,下列结论中正确的是( )
中,下列结论中正确的是( )
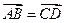
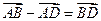
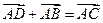
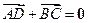
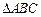 内一点,
内一点,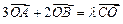 且
且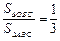 ,则
,则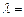 ________________.
________________.