Question

如图，四棱锥S—ABCD的底面是矩形，AB=a，AD=2，SA=1，且SA⊥底面ABCD，若边BC上存在异于B、C的一点P使得⊥.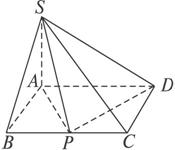

(1)求a的最大值;

(2)当a取最大值时,求异面直线AP与SD所成角的余弦值;

(3)当a取最大值时,求平面SCD的一个单位法向量.

Answer 1

解：(1)a=1.

(2)a=1时,P为BC中点,以A为原点,AB,AD,AS为x,y,z轴建立空间直角坐标系.则A(0,0,0),P(1,1,0),S(0,0,1),D(0,2,0).

∴=(1,1,0),=(0,2,-1),·=2.

∴cos〈,〉=.

∴异面直线AP与SD所成角的余弦值为.

(3)由(2)知:S(0,0,1),D(0,2,0),C(1,2,0),=(1,2,-1),=(-1,0,0).

设平面SCD的单位法向量n₀=(x,y,z),则

则∴

∴n₀=(0,,).