题目内容
已知锐角△ABC中的内角A、B、C的对边分别为a，b，c，定义向量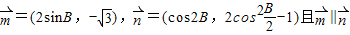
．（1）求函数f（x）=sin2xcosB-cos2xsinB的单调递增区间；
（2）如果b=2，求△ABC的面积的最大值．
【答案】分析：（1）通过
求出
，解出B的值，然后利用两角差的正弦函数化简函数f（x）=sin2xcosB-cos2xsinB为一个角的一个三角函数的形式，结合正弦函数的单调增区间，求出函数的单调递增区间；
（2）如果b=2，利用余弦定理得到ac的范围，然后确定△ABC的面积的最大值．
解答：解：（1）∵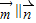
，∴
．∵
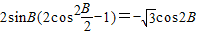，即
又∵B为锐角，∴2B∈（0，π），∴
，∴
.
．
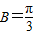由
．得：
．∴函数的单调递增区间为：
（2）∵
，由余弦定理
得到：ac+4=a2+c2≥2ac，∴ac≤4，
，（当且仅当a=c=2时等号成立）．
即△ABC面积的最大值为
．
点评：本题是中档题，考查三角函数的单调性，三角函数的恒等变换以及化简求值，余弦定理，函数最值的应用，考查计算能力．
求出，解出B的值，然后利用两角差的正弦函数化简函数f（x）=sin2xcosB-cos2xsinB为一个角的一个三角函数的形式，结合正弦函数的单调增区间，求出函数的单调递增区间；（2）如果b=2，利用余弦定理得到ac的范围，然后确定△ABC的面积的最大值．
解答：解：（1）∵
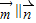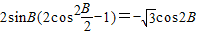，∴．∵，即又∵B为锐角，∴2B∈（0，π），∴
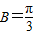，∴.．由
．得：．∴函数的单调递增区间为：（2）∵
，由余弦定理得到：ac+4=a2+c2≥2ac，∴ac≤4，，（当且仅当a=c=2时等号成立）．即△ABC面积的最大值为
．点评：本题是中档题，考查三角函数的单调性，三角函数的恒等变换以及化简求值，余弦定理，函数最值的应用，考查计算能力．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目