题目内容
某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,已知AB=AC=6km,现计划在BC边的高AO上一点P处建造一个变电站。记P到三个村庄的距离之和为y,
(Ⅰ)若∠PBO=α,把y表示成α的函数关系式;
(Ⅱ)变电站建于何处时,它到三个村庄的距离之和最小?
(Ⅰ)若∠PBO=α,把y表示成α的函数关系式;
(Ⅱ)变电站建于何处时,它到三个村庄的距离之和最小?
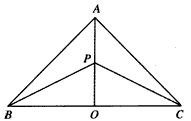
解:(Ⅰ)在Rt△AOB中,AB=6,所以OB=OA=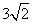 ,
,
所以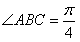 ,
,
由题意知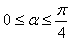 ,
,
所以点P到A,B,C的距离之和为
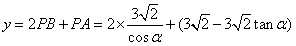
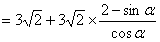 ,
,
故所求函数关系式为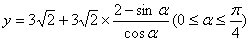 。
。
(Ⅱ)由(Ⅰ),得y′=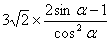 ,
,
令y′ =0,即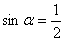 ,
,
又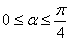 ,从而
,从而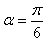 ,
,
当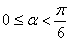 时,y′<0;当
时,y′<0;当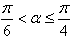 时,y′>0,
时,y′>0,
所以当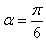 时,
时,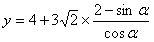 取得最小值,
取得最小值,
此时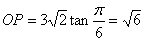 (km),
(km),
即点P在OA上距O点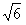 km处,
km处,
答:变电站建于距O点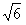 km处时,它到三个村庄的距离之和最小。
km处时,它到三个村庄的距离之和最小。
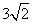 ,
,所以
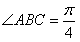 ,
,由题意知
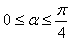 ,
,所以点P到A,B,C的距离之和为
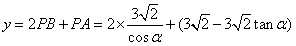
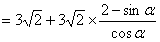 ,
,故所求函数关系式为
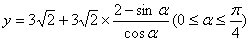 。
。(Ⅱ)由(Ⅰ),得y′=
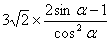 ,
,令y′ =0,即
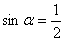 ,
,又
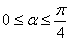 ,从而
,从而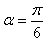 ,
,当
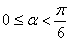 时,y′<0;当
时,y′<0;当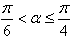 时,y′>0,
时,y′>0,所以当
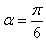 时,
时,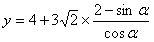 取得最小值,
取得最小值,此时
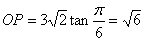 (km),
(km),即点P在OA上距O点
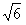 km处,
km处,答:变电站建于距O点
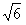 km处时,它到三个村庄的距离之和最小。
km处时,它到三个村庄的距离之和最小。
练习册系列答案
相关题目
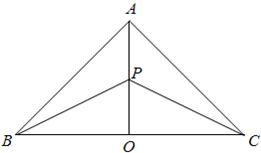 某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,已知AB=AC=6km,现计划在BC边的高AO上一点P处建造一个变电站.记P到三个村庄的距离之和为y.
某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,已知AB=AC=6km,现计划在BC边的高AO上一点P处建造一个变电站.记P到三个村庄的距离之和为y.
 ,把y表示成
,把y表示成 的函数关系式;(2)变电站建于何处时,它到三个小区的距离之和最小?
的函数关系式;(2)变电站建于何处时,它到三个小区的距离之和最小?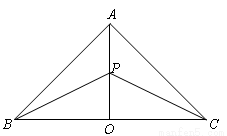
 ,求y关于
,求y关于 的函数关系式;
的函数关系式;