题目内容
已知数列{an},{bn}满足a1=1,a2=p(p是常数),bn=an·an+1,n∈N*,若{bn}是等比数列,甲同学说:{an}一定是等比数列;乙同学说:{an}一定不是等比数列.你认为他们的说法是否正确,为什么?
解:甲、乙两人的说法都不正确,理由如下:
设{bn}的公比为q,则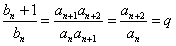 ,且q≠0,
,且q≠0,
又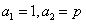 ,
,
∴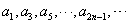 是以1为首项,p为公比的等比数列;
是以1为首项,p为公比的等比数列;
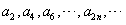 是以p为首项,q为公比的等比数列,
是以p为首项,q为公比的等比数列,
即数列{an}为:1,p,q,pq,q2,pq2,…,
当q=p2时,{an}是等比数列;
当q≠p2时,{an}不是等比数列。
设{bn}的公比为q,则
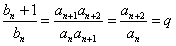 ,且q≠0,
,且q≠0,又
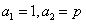 ,
,∴
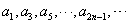 是以1为首项,p为公比的等比数列;
是以1为首项,p为公比的等比数列;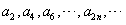 是以p为首项,q为公比的等比数列,
是以p为首项,q为公比的等比数列,即数列{an}为:1,p,q,pq,q2,pq2,…,
当q=p2时,{an}是等比数列;
当q≠p2时,{an}不是等比数列。

练习册系列答案
相关题目