Question

【题目】如图，在三棱柱中，点P，G分别是，的中点，已知⊥平面ABC，==3，==2.

（I）求异面直线与AB所成角的余弦值；

（II）求证：⊥平面；

（III）求直线与平面所成角的正弦值.

Answer 1

【答案】（Ⅰ）（Ⅱ）见解析（Ⅲ）

【解析】分析：（Ⅰ）由题意得∥AB，故∠G是异面直线与AB所成的角，解三角形可得所求余弦值．（Ⅱ）在三棱柱中，由⊥平面ABC可得⊥A1G，于是⊥A1G，又A1G⊥，根据线面垂直的判定定理可得结论成立．（Ⅲ）取的中点H，连接AH，HG；取HG的中点O，连接OP，．由PO//A1G可得平面，

故得∠PC1O是PC1与平面所成的角，然后解三角形可得所求．

详解：

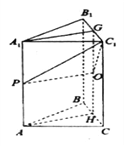
(I)∵∥AB，

∴∠G是异面直线与AB所成的角．

∵==2，G为BC的中点，

∴A1G⊥B1C1，

在中，，

∴，

即异面直线AG与AB所成角的余炫值为．

（II）在三棱柱中，

∵⊥平面ABC，平面ABC，

∴⊥A1G，

∴⊥A1G，

又A1G⊥，，

∴平面．

（III）解：取的中点H，连接AH，HG；取HG的中点O，连接OP，．

∵PO//A1G，

∴平面，

∴∠PC1O是PC1与平面所成的角．

由已知得，，

∴

∴直线与平面所成角的正弦值为．