题目内容
如果θ是第二象限角,且满足cos
-sin
=
,那么
( )
| θ |
| 2 |
| θ |
| 2 |
| 1-sinθ |
| θ |
| 2 |
| A、是第一象限角 |
| B、是第三象限角 |
| C、可能是第一象限角,也可能是第三象限角 |
| D、是第二象限角 |
分析:先根据θ的范围确定
的范围,再由cos
-sin
=
可确定cos
与sin
的大小关系,进而确定
的象限.
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| 1-sinθ |
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
解答:解:∵θ是第二象限角∴
+2kπ<θ<π+2kπ∴
+kπ<
<
+kπ(k∈Z)
∴当k为偶数时,
在第一象限;当k为奇数时,
在第三象限;
∵
=
=|cos
-sin
|=cos
-sin
∴cos
>sin
∴
是第三象限角
故选B.
| π |
| 2 |
| π |
| 4 |
| θ |
| 2 |
| π |
| 2 |
∴当k为偶数时,
| θ |
| 2 |
| θ |
| 2 |
∵
| 1-sinθ |
(sin
|
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
∴cos
| θ |
| 2 |
| θ |
| 2 |
∴
| θ |
| 2 |
故选B.
点评:本题主要考查象限角和二倍角公式以及同角三角函数的基本关系.属基础题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
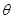 是第二象限角,且
是第二象限角,且 ,那么
,那么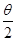 所在象限为第几象限
所在象限为第几象限