题目内容
已知函数 满足对任意x1≠x2,都有
满足对任意x1≠x2,都有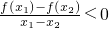 成立,则实数a的取值范围是
成立,则实数a的取值范围是
- A.(0,1)
- B.

- C.

- D.

C
分析:由对任意x1≠x2,都有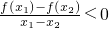 成立可知函数为单调递减函数,则函数g(x)=(3a-2)x+6a-1在(-∞,1)单调递减,h(x)=ax在[1,+∞)单调递减且g(1)≥h(1),从而可求a的范围
成立可知函数为单调递减函数,则函数g(x)=(3a-2)x+6a-1在(-∞,1)单调递减,h(x)=ax在[1,+∞)单调递减且g(1)≥h(1),从而可求a的范围
解答:∵对任意x1≠x2,都有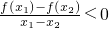 成立
成立
即x1<x2时,f(x1)>f(x2)
由函数的单调性的定义可知函数为单调递减函数
∵ 单调递减
单调递减
∴函数g(x)=(3a-2)x+6a-1在(-∞,1)单调递减,h(x)=ax在[1,+∞)单调递减且g(1)≥h(1)
∴
∴
∴
故选C
点评:本题主要考查了函数的单调性的定义的应用,分段函数的单调性的应用,解题的关键是熟练应用指数函数与一次函数的单调性的条件.
分析:由对任意x1≠x2,都有
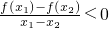 成立可知函数为单调递减函数,则函数g(x)=(3a-2)x+6a-1在(-∞,1)单调递减,h(x)=ax在[1,+∞)单调递减且g(1)≥h(1),从而可求a的范围
成立可知函数为单调递减函数,则函数g(x)=(3a-2)x+6a-1在(-∞,1)单调递减,h(x)=ax在[1,+∞)单调递减且g(1)≥h(1),从而可求a的范围解答:∵对任意x1≠x2,都有
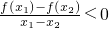 成立
成立即x1<x2时,f(x1)>f(x2)
由函数的单调性的定义可知函数为单调递减函数
∵
 单调递减
单调递减∴函数g(x)=(3a-2)x+6a-1在(-∞,1)单调递减,h(x)=ax在[1,+∞)单调递减且g(1)≥h(1)
∴

∴

∴

故选C
点评:本题主要考查了函数的单调性的定义的应用,分段函数的单调性的应用,解题的关键是熟练应用指数函数与一次函数的单调性的条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目