题目内容
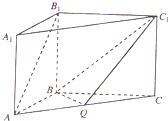 (2013•唐山二模)如图,直三棱柱ABC-A1B1C1中,AB=BC,∠ABC=120°,Q是AC上的点,AB1∥平面BC1Q.
(2013•唐山二模)如图,直三棱柱ABC-A1B1C1中,AB=BC,∠ABC=120°,Q是AC上的点,AB1∥平面BC1Q.(Ⅰ)确定点Q在AC上的位置;
(Ⅱ)若QC1与平面BB1C1C所成角的正弦值为
| ||
| 4 |
分析:(I)连接B1C交BC1于点P,连接PQ.利用线面平行的性质定理及直线AB1∥平面BC1Q,可得AB1∥PQ.再利用线线平行的性质定理及P为B1C的中点即可得到Q为AC的中点.
(II)如图建立空间直角坐标系,设AB=BC=a,BB1=b,利用斜线的方向向量与法向量的夹角及两个平面的法向量的夹角即可得出.
(II)如图建立空间直角坐标系,设AB=BC=a,BB1=b,利用斜线的方向向量与法向量的夹角及两个平面的法向量的夹角即可得出.
解答: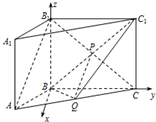 解:(Ⅰ)连接B1C交BC1于点P,连接PQ.
解:(Ⅰ)连接B1C交BC1于点P,连接PQ.
因为直线AB1∥平面BC1Q,AB1?平面AB1C,平面BC1Q∩平面AB1C=PQ,
所以AB1∥PQ.
因为P为B1C的中点,且AB1∥PQ,
所以,Q为AC的中点.
(II)如图建立空间直角坐标系,设AB=BC=a,BB1=b,则平面BC1C的法向量
=(1,0,0).
B(0,0,0),C1(0,a,b),Q(
a,
a,0),
∴
=(0,a,b),
=(-
a,
a,b).
∵QC1与平面BC1C所成角的正弦值为
,
∴
=|cos<
,
>|=
=
,化为3a2=4b2,取b=
a.
设平面C1BQ的法向量为
=(x,y,z),则
,即
,及b=
a.
令x=1,解得y=-
,z=2,∴
=(1,-
,2).
∴cos<
,
>=
=
=
.
故二面角Q-BC1-C的余弦值为
.
 解:(Ⅰ)连接B1C交BC1于点P,连接PQ.
解:(Ⅰ)连接B1C交BC1于点P,连接PQ.因为直线AB1∥平面BC1Q,AB1?平面AB1C,平面BC1Q∩平面AB1C=PQ,
所以AB1∥PQ.
因为P为B1C的中点,且AB1∥PQ,
所以,Q为AC的中点.
(II)如图建立空间直角坐标系,设AB=BC=a,BB1=b,则平面BC1C的法向量
| m |
B(0,0,0),C1(0,a,b),Q(
| ||
| 4 |
| 1 |
| 4 |
∴
| BC1 |
| QC1 |
| ||
| 4 |
| 3 |
| 4 |
∵QC1与平面BC1C所成角的正弦值为
| ||
| 4 |
∴
| ||
| 4 |
| QC1 |
| m |
|
| ||||
|
|
| ||||||
|
| ||
| 2 |
设平面C1BQ的法向量为
| n |
|
|
| ||
| 2 |
令x=1,解得y=-
| 3 |
| n |
| 3 |
∴cos<
| m |
| n |
| ||||
|
|
| 1 | ||
|
| ||
| 4 |
故二面角Q-BC1-C的余弦值为
| ||
| 4 |
点评:本题综合考查了线面平行的性质定理、通过建立空间直角坐标系利用平面的法向量求二面角的余弦值及线面角等基础知识与基本技能,考查了空间想象能力、推理能力和计算能力.

练习册系列答案
相关题目