Question

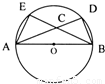
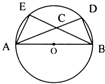如图AB是圆O的直径，过A、B的两条弦AD和BE相交于点C，若圆O的半径是3，那么AC•AD+BC•BE的值等于

36

．

Answer 1

分析：连接AE，BD，过C作CF⊥AB，与AB交于F，得出A，F，C，E四点共圆，BC•BE=BF•BA，同理可证F，B，D，C四点共圆，AC•AD=AF•AB，两式相加，转化为直径BA表达式求解即可．

解答：解：连接AE，BD，过C作CF⊥AB，与AB交于F，

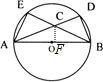
∵AB是圆的直径，
∴∠AEB=∠ADB=90°，
∵∠AFC=90°，∴A，F，C，E四点共圆．
∴BC•BE=BF•BA（1）
同理可证F，B，D，C四点共圆
∴AC•AD=AF•AB（2）
（1）+（2）得AC•AD+BC•BE=（BF+AF）•BA=BA2
圆O的半径是3，直径BA=6
所以AC•AD+BC•BE=62=36
故答案为：36

点评：本题考查与圆有关的线段，割线定理的应用，根据所求的不等式，构造四点共圆是本题的关键．