题目内容

如图,AB是圆O的直径,C是圆O上的点,PA垂直于圆O所在的平面,AE⊥PB于E,AF⊥PC于F,求证:平面AEF⊥平面PAB,平面AEF⊥平面PBC.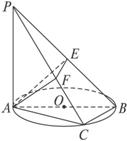

证明:∵AB是圆O的直径,∴BC⊥AC.

又∵PA⊥平面ABC,∴BC⊥PA.∴BC⊥平面PAC.BC平面PBC,

∴平面PAC⊥平面PBC.

由AF⊥PC可得AF⊥平面PBC.

∴AF⊥PB.再由PB⊥AE可知PB⊥平面AEF,PB平面PAB,PB平面PBC,∴平面AEF⊥平面PAB,且平面AEF⊥平面PBC.

练习册系列答案

寒假生活宁夏人民教育出版社系列答案

全优假期作业本快乐寒假系列答案

新路学业快乐假期寒假总复习系列答案

举一反三期末百分冲刺卷系列答案

假期生活寒假方圆电子音像出版社系列答案

百年学典快乐假期寒假作业系列答案

复习大本营期末假期复习一本通寒假系列答案

五州图书超越假期寒假系列答案

特优复习计划期末冲刺寒假作业教材衔接系列答案

中考热点试题分类全解系列答案

相关题目

（理科）如图的多面体是底面为平行四边形的直四棱柱ABCD-A₁B₁C₁D₁，经平面AEFG所截后得到的图形．其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°．

（Ⅰ）求证：BD⊥平面ADG；
（Ⅱ）求平面AEFG与平面ABCD所成锐二面角的余弦值．

（文科）如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD所在的平面和圆O所在的平面互相垂直，且AB=2，AD=EF=1．
（Ⅰ）求证：AF⊥平面CBF；
（Ⅱ）设FC的中点为M，求证：OM∥平面DAF．

如图，直三棱柱的一个底面ABC内接于圆O，AB是圆O的直径．
（1）求证：平面ACD⊥平面ADE；
（2）若AB=2，BC=1，tan∠EAB=

，求几何体EDABC的体积V．

（理科）如图的多面体是底面为平行四边形的直四棱柱ABCD-A₁B₁C₁D₁，经平面AEFG所截后得到的图形．其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60°．

（Ⅰ）求证：BD⊥平面ADG；
（Ⅱ）求平面AEFG与平面ABCD所成锐二面角的余弦值．

（文科）如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD所在的平面和圆O所在的平面互相垂直，且AB=2，AD=EF=1．
（Ⅰ）求证：AF⊥平面CBF；
（Ⅱ）设FC的中点为M，求证：OM∥平面DAF．

如图，直三棱柱的一个底面ABC内接于圆O，AB是圆O的直径．
（1）求证：平面ACD⊥平面ADE；
（2）若AB=2，BC=1，

，求几何体EDABC的体积V．

A．（参数方程与极坐标）

直线与直线的夹角大小为

B．（不等式选讲）要使关于x的不等式在实数

范围内有解，则A的取值范围是

C．（几何证明选讲）如图所示，在圆O中，AB是圆O的直

径AB =8,E为OB．的中点，CD过点E且垂直于AB,

EF⊥AC,则

CF•CA=