题目内容
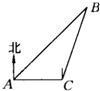
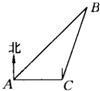 如图所示,一艘轮船在A处观测到北偏东45°方向上有一个灯塔B,轮船在正东方向以每小时20海里的速度航行1.5小时后到达C处,又观测到灯塔B在北偏东15°方向上,则此时轮船与灯塔B相距
如图所示,一艘轮船在A处观测到北偏东45°方向上有一个灯塔B,轮船在正东方向以每小时20海里的速度航行1.5小时后到达C处,又观测到灯塔B在北偏东15°方向上,则此时轮船与灯塔B相距
分析:作CD⊥AB,垂足为D.构建直角三角形后,利用已知角∠CAB的正弦值,以及CA的长,可求出CD.然后放到直角三角形BCD中,根据30°的角对的直角边是斜边的一半,求出BC.
解答: 解:作CD⊥AB,垂足为D.
解:作CD⊥AB,垂足为D.
根据题意,得∠BAC=45°,∠1=15°,
∴∠ACB=105°,
则∠B=30°,AC=20×1.5=30(海里),
在Rt△ADC中,∠BAC=45°,AC=30,
∴CD=AC•sin45°=30×
=15
(海里).
在Rt△BCD中,∠B=30°,CD=15
,
∴BC=30
(海里).
此时轮船与灯塔B相距30
海里.
故答案为:30
.
 解:作CD⊥AB,垂足为D.
解:作CD⊥AB,垂足为D.根据题意,得∠BAC=45°,∠1=15°,
∴∠ACB=105°,
则∠B=30°,AC=20×1.5=30(海里),
在Rt△ADC中,∠BAC=45°,AC=30,
∴CD=AC•sin45°=30×
| ||
| 2 |
| 2 |
在Rt△BCD中,∠B=30°,CD=15
| 2 |
∴BC=30
| 2 |
此时轮船与灯塔B相距30
| 2 |
故答案为:30
| 2 |
点评:解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
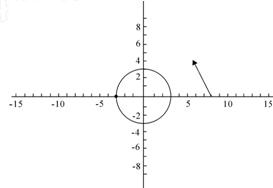 一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西80km处,受影响的范围是半径长为r(r>0)km的圆形区域.轮船的航行方向为西偏北45°且不改变航线,假设台风中心不移动. 如图所示,试问:
一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西80km处,受影响的范围是半径长为r(r>0)km的圆形区域.轮船的航行方向为西偏北45°且不改变航线,假设台风中心不移动. 如图所示,试问: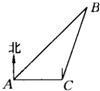 如图所示,一艘轮船在A处观测到北偏东45°方向上有一个灯塔B,轮船在正东方向以每小时20海里的速度航行1.5小时后到达C处,又观测到灯塔B在北偏东15°方向上,则此时轮船与灯塔B相距 ________海里.(结果保留根号)
如图所示,一艘轮船在A处观测到北偏东45°方向上有一个灯塔B,轮船在正东方向以每小时20海里的速度航行1.5小时后到达C处,又观测到灯塔B在北偏东15°方向上,则此时轮船与灯塔B相距 ________海里.(结果保留根号)