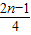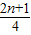题目内容
命题:公差不为0的等差数列的通项可以表示为关于n的一次函数形式,反之通项是关于n的一次函数形式的数列为等差数列为真,现有正项数列{an}的前n项和是Sn,若{an}和{
}都是等差数列,且公差相等,则数列{an}的一个通项公式为( )
| Sn |
分析:设出等差数列的首项和公差,写出其前n项和公式,再由{
}都是等差数列写出通项公式,两边平方后由Sn相等列式,并有等式恒成立求出d的值,进一步求出首项,则答案可求.
| Sn |
解答:解:设正项数列{an}的公差为d,首项a1,
Sn=na1+
,
=
+(n-1)d=
+(n-1)d
平方得,
Sn=a1+2
(n-1)d+(n-1)2d2
na1+
=a1+2
(n-1)d+(n-1)2d2.
整理得,n(
-d2)=2
d-d2-a1,
因为对任意n∈N+都成立,所以
-d2=0,又d≠0.
所以d=
,代入2
d-d2-a1=0得a1=
.
所以an=a1+(n-1)d=
+
(n-1)=
.
故选A.
Sn=na1+
| n(n-1)d |
| 2 |
| Sn |
| S1 |
| a1 |
平方得,
Sn=a1+2
| a1 |
na1+
| n(n-1)d |
| 2 |
| a1 |
整理得,n(
| d |
| 2 |
| a1 |
因为对任意n∈N+都成立,所以
| d |
| 2 |
所以d=
| 1 |
| 2 |
| a1 |
| 1 |
| 4 |
所以an=a1+(n-1)d=
| 1 |
| 4 |
| 1 |
| 2 |
| 2n-1 |
| 4 |
故选A.
点评:本题考查了等差数列的通项公式,训练了利用等式恒成立求系数的值,考查了计算能力,是中档题.

练习册系列答案
相关题目
已知公差不为0的等差数列{an}满足a1,a3,a4成等比关系,Sn为{an}的前n项和,则
的值为( )
| S3-S2 |
| S5-S3 |
| A、2 | ||
| B、3 | ||
C、
| ||
| D、不存在 |
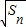 }都是等差数列,且公差相等,则数列{an}的一个通项公式为( )
}都是等差数列,且公差相等,则数列{an}的一个通项公式为( )