Question

（本题满分12分）如图，在平面直角坐标系xOy中，AB是半圆⊙O：x² + y² = 1（y≥0）的直径，C是半圆O（除端点A、B）上的任意一点，在线段AC的延长线上取点P，使︱PC︱=︱BC︱，试求动点P 的轨迹方程．

 

Answer 1

解   连结BP，由已知得∠APB = 45°．                           …………………… 2分

设P（x，y），则 ，，由PA到PB的角为45°，

得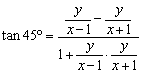，化简得 x² +（y－1）² = 2．      …………………… 10分

由已知，y＞0且＞0，故点P的轨迹方程为x² +（y－1）² = 2（x＞－1，y＞0）．                                                                                  …………………… 12分

法二  连结BP，由已知可得∠APB = 45°，∴ 点P在以AB为弦，所对圆周角为45°的圆上．

设该圆的圆心为D，则点D在弦AB的中垂线上，即y轴上，且∠ADB = 90°，∴ D（0，1），︱DA︱=，圆D的方程为x² +（y－1）² = 2．

由已知，当点C趋近于点B时，点P趋近于点B；当点C趋近于点A时，点P趋近于点（－1，2），所以点P的轨迹方程为x² +（y－1）² = 2（x＞－1，y＞0）．