题目内容
 已知双曲线C:
已知双曲线C: +
+ =1(a>0,b>0),B是右顶点,F是右焦点,点A在x轴正半轴上,且满足|
=1(a>0,b>0),B是右顶点,F是右焦点,点A在x轴正半轴上,且满足| |、|
|、| |、|
|、| |成等比数列,过F作双曲线C在第一、第三象限的渐近线的垂线l,垂足为P.
|成等比数列,过F作双曲线C在第一、第三象限的渐近线的垂线l,垂足为P.
(1)求证: •
• =
= •
•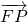 ;
;
(2)若l与双曲线C的左、右两支分别相交于点D、E,求双曲线C的离心率e的取值范围.
 解:(1)l:
解:(1)l: ,
,
解得
 ,
, .
.∵
 、
、 、
、 成等比数列,
成等比数列,∴
 ∴
∴ =
=
 ,
, ,
, ,
, ,
,∴
 ,
, .
.∴

(2)
 ,
,∴
 .
.即
 ,
,∵
 ,
,∴b4>a4,即b2>a2,c2-a2>a2.∴e2>2,即
 .
.分析:(1)依题意可表示出l的方程,与渐近线方程联立求得交点P的坐标,根据
 、
、 、
、 成等比数列,求得A的坐标,进而表示出
成等比数列,求得A的坐标,进而表示出 ,
, 和
和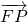 ,进而求得
,进而求得 和
和 进而可知
进而可知 .
.(2)把直线l的方程与双曲线方程联立,进而根据韦达定理表示出x1•x2根据其小于0,求得a和c的不等式关系求得e的范围.
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生综合分析问题和对圆锥曲线基础知识的灵活运用.

练习册系列答案
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,右准线方程为x=
,右准线方程为x=
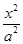 -
- =1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为(
)
=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为(
) -
-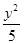 =1
B.
=1
B.  -
- =1 C.
=1 C.  -
- =1
=1 -
- =1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为
=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为 -
- =1 B、
=1 B、 -
- =1
C、
=1
C、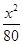 -
- =1[w~#
=1[w~#