题目内容
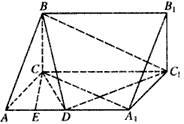
如图,三棱柱ABC-A1B1C1中,BC⊥侧面AA1C1C,AC=BC=1,CC1=2, ,D为AA1的中点。
,D为AA1的中点。
 ,D为AA1的中点。
,D为AA1的中点。
(1)求证:A1C⊥平面ABC;
(2)截面BDC1将三棱柱分成两部分,其体积分别是V1,V2,求V1:V2。
(2)截面BDC1将三棱柱分成两部分,其体积分别是V1,V2,求V1:V2。
解:(1)∵BC⊥侧面AA1C1C,A1C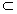 面AA1C1C, 面AA1C1C, ∴BC⊥A1C 在△AA1C中,AC=1,AA1=CC1=2, 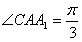 由余弦定理得A1C2=AC2+AA12-2AC·AA1cos∠CAA1 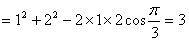 所以 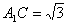 故有 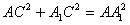 , ,所以AC⊥A1C, 而AC∩BC=C, ∴A1C⊥平面ABC。 |
|
| (2)∵BC⊥侧面AA1C1C, ∴BC⊥AC, 故Rt△ABC的面积 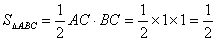 由(1)知A1C⊥平面ABC, ∴棱柱ABC- A1B1C1的体积 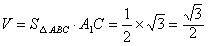 截面BDC1将三棱柱分成两部分,设V1对应的是四棱锥B-ADC1C 如图,过点C作CE⊥AD,垂足为E 在Rt△CAE中,CE=AC·sin∠CAE= 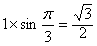 所以梯形ADC1C的面积为 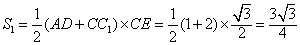 ∵BC⊥侧面AA1C1C, ∴四棱锥B-ADC1C的体积 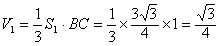 故另一部分体积 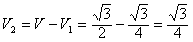 所以 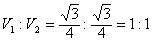 。 。 |
 |

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目

 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC. (2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
(2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC= 如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB
如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB (2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=
(2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=