题目内容
已知函数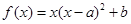 在
在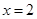 处有极大值.
处有极大值.
(Ⅰ)求 的值;
的值;
(Ⅱ)若过原点有三条直线与曲线 相切,求
相切,求 的取值范围;
的取值范围;
(Ⅲ)当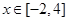 时,函数
时,函数 的图象在抛物线
的图象在抛物线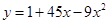 的下方,求
的下方,求 的取值范围.
的取值范围.
(Ⅰ)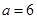 (Ⅱ)
(Ⅱ)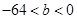 (Ⅲ)
(Ⅲ)
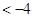
解析试题分析:(Ⅰ)通过对函数f(x)求导,根据函数在x=2处有极值,可知f'(2)=0,解得a的值.
(Ⅱ)把(1)求得的a代入函数关系式,设切点坐标,进而根据导函数可知切线斜率,则切线方程可得,整理可求得b的表达式,令g'(x)=0解得x1和x2.进而可列出函数g(x)的单调性进而可知-64<b<0时,方程b=g(x)有三个不同的解,结论可得.
(Ⅲ)当x∈[-2,4]时,函数y=f(x)的图象在抛物线y=1+45x-9x2的下方,进而可知x3-12x2+36x+b<1+45x-9x2在x∈[-2,4]时恒成立,整理可得关于b的不等式,令h(x)=-x3+3x2+9x+1,对h(x)进行求导由h'(x)=0得x1和x2.分别求得h,h(-1),h(3),h(4),进而可知h(x)在[-2,4]上的最小值是,进而求得b的范围.
试题解析:(Ⅰ)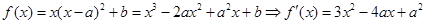 ,
,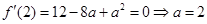 或
或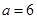 ,
,
当 时,函数在
时,函数在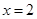 处取得极小值,舍去;
处取得极小值,舍去;
当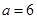 时,
时,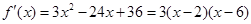 ,函数在
,函数在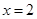 处取得极大值,符合题意,∴
处取得极大值,符合题意,∴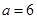 .(3分)
.(3分)
(Ⅱ)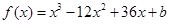 ,设切点为
,设切点为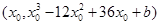 ,则切线斜率为
,则切线斜率为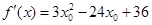 ,切线方程为
,切线方程为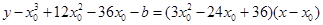 ,
,
即 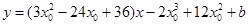 ,
,
∴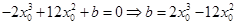 .
.
令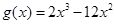 ,则
,则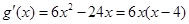 ,
,
由 得,
得,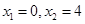 .
.
函数 的单调性如下:
的单调性如下:


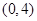

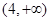
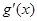


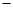




变式训练系列答案
博师在线系列答案
灿烂在六月模拟强化测试精编系列答案
测试卷全新升级版系列答案
测试新方案系列答案
常德标准卷系列答案
超级奥赛培优竞赛系列答案
超级考卷系列答案
超级培优系列答案
超级英语系列答案
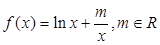 .
.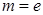 (
(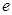 为自然对数的底数)时,求
为自然对数的底数)时,求 的最小值;
的最小值;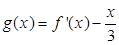 零点的个数;
零点的个数;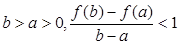 恒成立,求
恒成立,求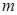 的取值范围.
的取值范围.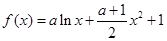 .
.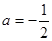 时,求
时,求 在区间
在区间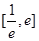 上的最值;
上的最值;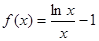
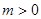 ,求
,求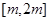 上的最大值;
上的最大值;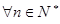 ,不等式
,不等式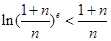 .
.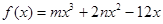 的减区间是(-2,2)
的减区间是(-2,2)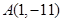 且与曲线
且与曲线 相切的切线方程;
相切的切线方程;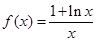 .
.
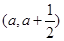 其中a >0,上存在极值,求实数a的取值范围;
其中a >0,上存在极值,求实数a的取值范围;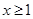 时,不等式
时,不等式 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.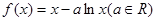
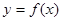 在点
在点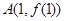 处的切线方程;
处的切线方程; 的极值.
的极值. ,则
,则 的展开式中的常数项是 (用数字作答).
的展开式中的常数项是 (用数字作答). 在点(1,-1)处的切线方程是 .
在点(1,-1)处的切线方程是 .