题目内容
设F为抛物线y=-
x2的焦点,与抛物线相切于点P(-4,-4)的直线l与x轴的交点为Q,则∠PQF等于( )
| 1 |
| 4 |
| A、30° | B、45° |
| C、60° | D、90° |
分析:先求出F的坐标,利用导数求直线l的斜率,点斜式写出直线l的方程,由此方程求出直线l与x轴的交点Q的坐标,计算kQF
的值,由斜率之积等于-1得到PQ⊥QF.
的值,由斜率之积等于-1得到PQ⊥QF.
解答:解:易知F(0,-1),又y′=-
x,所以kPQ=2,所以,直线l的方程为y+4=2(x+4),
令y=0,得Q(-2,0),所以,kQF=
=-
,所以PQ⊥QF,即∠PQF=90°,
故选 D.
| 1 |
| 2 |
令y=0,得Q(-2,0),所以,kQF=
| -1-0 |
| 0+2 |
| 1 |
| 2 |
故选 D.
点评:本题考查利用导数求直线的斜率、用点斜式写直线的方程,以及利用两直线垂直的条件判断两直线垂直.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
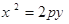
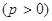 的焦点,A、B、C为该抛物线上三点,已知
的焦点,A、B、C为该抛物线上三点,已知 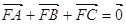 且
且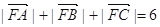 .
. 相交于点Q。证明以PQ为直径的圆恒过y轴上某定点。
相交于点Q。证明以PQ为直径的圆恒过y轴上某定点。