题目内容
已知数列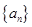 满足:
满足: ,其中
,其中 .
.
(1)求证:数列 是等比数列;
是等比数列;
(2)令 ,求数列
,求数列 的最大项.
的最大项.
(1)详见解析;(2)最大项为 .
.
解析试题分析:(1)首先根据已知等式 ,令
,令 ,可得
,可得 ,再根据已知等式可得
,再根据已知等式可得 ,将两式相减,即可得到数列
,将两式相减,即可得到数列 的一个递推公式,只需验证将此递推公式变形得到形如
的一个递推公式,只需验证将此递推公式变形得到形如 的形式,从可证明数列
的形式,从可证明数列 是等比数列;(2)由(1)可得
是等比数列;(2)由(1)可得 ,从而
,从而 ,因此要求数列
,因此要求数列 的最大项,可以通过利用作差法判断数列
的最大项,可以通过利用作差法判断数列 的单调性来求得:
的单调性来求得: ,
,
当 时,
时, ,即
,即 ;当
;当 时,
时, ; 当
; 当 时,
时, ,即
,即 ,因此数列
,因此数列 的最大项为
的最大项为 .
.
试题解析:(1)当 时,
时, ,∴
,∴ , 1分
, 1分
又∵ , 2分
, 2分
∴ ,即
,即 ,∴
,∴ . 4分
. 4分
又∵ ,∴数列
,∴数列 是首项为
是首项为 ,公比为
,公比为 的等比数列; 6分
的等比数列; 6分
(2)由(1)知, ,
,
∴ , ∴
, ∴ , 8分
, 8分
当 时,
时, ,即
,即 , 9分
, 9分
当 时,
时, , 10分
, 10分
当 时,
时, ,即
,即 , 11分
, 11分
∴数列 的最大项为
的最大项为 , 13分
, 13分
考点:1.数列的通项公式;2.数列的单调性判断.

练习册系列答案
相关题目
 是首相大于零的等比数列,则“
是首相大于零的等比数列,则“ ”是“数列
”是“数列 ,过点P(-2,-4)的直线
,过点P(-2,-4)的直线  的参数方程为:
的参数方程为: (t为参数),直线
(t为参数),直线 成等比数列,求a的值
成等比数列,求a的值 为等比数列,
为等比数列, ,记
,记 .
. 和
和 ;
;
 ,有
,有 成立.
成立. =an·an+2k成立,则称数列{an}为“Jk型”数列.
=an·an+2k成立,则称数列{an}为“Jk型”数列. 满足
满足 ,
, .
. ,求数列
,求数列 的前
的前 项和
项和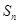 .
. 满足
满足 =
= ,若
,若 =
= ,则
,则 =____________
=____________ 的前
的前 项和为
项和为 ,若
,若 ,则
,则 ___________
___________