题目内容
若复数z满足z(1+i)=1-i(i是虚数单位),求|z|和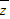 .
.
【答案】分析:根据复数乘法法则,在等式的两边都乘以1-i,化简整理可得z=-i,由此即可得到|z|和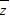 的值.
的值.
解答:解:∵z(1+i)=1-i
∴等式两边都乘以1-i,得(1+i)(1-i)z=(1-i)2
即2z=(1-i)2=1-2i+i2=-2i
∴z=-i,可得|z|=1,且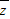 =i.
=i.
点评:本题给出复数z满足的等式,求复数的模和它的共轭复数,着重考查了复数的基本概念和四则运算等知识,属于基础题.
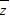 的值.
的值.解答:解:∵z(1+i)=1-i
∴等式两边都乘以1-i,得(1+i)(1-i)z=(1-i)2
即2z=(1-i)2=1-2i+i2=-2i
∴z=-i,可得|z|=1,且
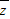 =i.
=i.点评:本题给出复数z满足的等式,求复数的模和它的共轭复数,着重考查了复数的基本概念和四则运算等知识,属于基础题.

练习册系列答案
相关题目
若复数 z 满足z•(1+i)=1-i(i是虚数单位),则z的共轭复数
=( )
. |
| z |
| A、i | B、-i | C、1+i | D、1-i |
i是虚数单位,若复数z满足z(1+i)=1-i,则复数z的实部与虚部的和是( )
| A、0 | B、-1 | C、1 | D、2 |