题目内容
设向量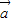 =(2sinx,
=(2sinx,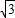 cosx),
cosx),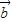 =(cosx,2cosx).
=(cosx,2cosx).(1)求函数f(x)=
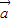 •
•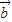 -
-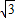 的最小正周期;
的最小正周期;(2)作出函数y=f(x)在[-
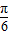 ,
,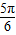 ]的简图.
]的简图.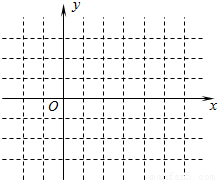
【答案】分析:(1)利用两角和的正弦公式,二倍角公式,把函数y化为2sin(2x+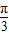 )即可得到最小正周期;
)即可得到最小正周期;
(2)让2x+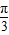 =0,
=0,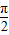 ,π,
,π,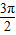 ,2π,分别求出x及对应y值,描点作图即可.
,2π,分别求出x及对应y值,描点作图即可.
解答:解:(1)f(x)=2sinxcosx+2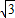 cos2x-
cos2x-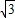
=sin2x+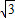 (1+cos2x)-
(1+cos2x)-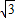
=2sin(2x+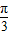 )(3分)
)(3分)
最小正周期T=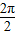 =π
=π
(2)列表
画图:
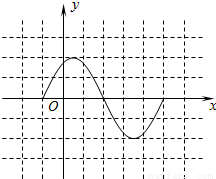
点评:本题考查两角和的正弦公式,二倍角公式,正弦函数的周期性,把函数y化为2sin(2x+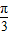 ),是解题的关键.
),是解题的关键.
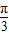 )即可得到最小正周期;
)即可得到最小正周期;(2)让2x+
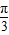 =0,
=0,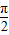 ,π,
,π,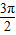 ,2π,分别求出x及对应y值,描点作图即可.
,2π,分别求出x及对应y值,描点作图即可.解答:解:(1)f(x)=2sinxcosx+2
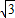 cos2x-
cos2x-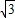
=sin2x+
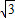 (1+cos2x)-
(1+cos2x)-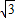
=2sin(2x+
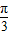 )(3分)
)(3分)最小正周期T=
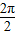 =π
=π (2)列表
| x | -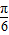 | 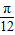 | 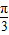 | 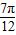 | 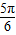 |
2x+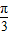 | 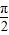 | π | 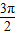 | 2π | |
| y | 2 | -2 |

点评:本题考查两角和的正弦公式,二倍角公式,正弦函数的周期性,把函数y化为2sin(2x+
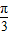 ),是解题的关键.
),是解题的关键. 
练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
 设向量
设向量