题目内容

如图，直线l⊥FH于H，O为FH的中点，曲线C1，C2是以F为焦点，l为准线的圆锥曲线（图中只画出曲线的一部分），那么圆锥曲线C1是
椭圆
椭圆
； 圆锥曲线C2是
双曲线
双曲线
．
分析：设曲线C1，C2与直线FH的交点分别为A、B，可得曲线C1的离心率e1=
|AF|
|AH|
∈（0，1），曲线C2的离心率e2=
|BF|
|BH|
∈（1，+∞），可得曲线的种类．
解答：解：设曲线C1，C2与直线FH的交点分别为A、B，
可得曲线C1的离心率e1=
|AF|
|AH|
，
由与O为FH的中点，显然有|AF|＜|AH|，
故e1=
|AF|
|AH|
∈（0，1），故曲线C1为椭圆；
同理可得曲线C2的离心率e2=
|BF|
|BH|
，
可得e2∈（1，+∞），故曲线C2为双曲线；
故答案为：椭圆；  双曲线；
点评：本题考查双曲线和椭圆的简单性质，涉及曲线的离心率的取值范围问题，属中档题．
练习册系列答案
相关题目
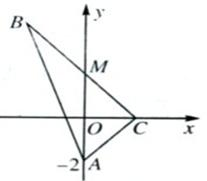精英家教网如图所示，在△ABC中，
CA
⊥
CB
，
OA
=(0，-2)，M在y轴上，且
AM
=
1
2
(
AB
+
AC
)，C在x轴上移动．
（Ⅰ）求点B的轨迹E的方程；
（Ⅱ）过点F(0，-
1
4
)的直线l交轨迹E于H，G两点（H在F，G之间），若
FH
=
1
2
HG
，求直线l的斜率．
（2006•石景山区一模）如图所示，已知圆C：（x+1）2+y2=8，定点A（1，0），M为圆上一动点，点P在AM上，点N在CM上，且满足
AM
=2
AP
，
NP
•
AM
=0，点N的轨迹为曲线E．
（Ⅰ） 求曲线E的方程；
（Ⅱ） 若点B1（x1，y1），B2（-1，y2），B3（x3，y3）在曲线E上，线段B1B3的垂直平分线为直线l，且|B1A|，|B2A|，|B3A|成等差数列，求x1+x3的值，并证明直线l过定点；
（Ⅲ）若过定点F（0，2）的直线交曲线E于不同的两点G、H（点G在点F、H之间），且满足
FG
=λ
FH
，求λ的取值范围．
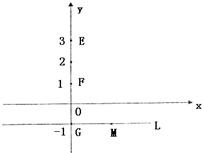精英家教网如图，O是坐标原点，已知三点E（0，3），F（0，1），G（0，-1），直线L：y=-1，M是直线L上的动点，H．P是坐标平面上的动点，且
FH
=
HM
，
PM
=λ
EG
，
PH
•
FM
=0．
（Ⅰ）求动点P的轨迹方程；
（Ⅱ）过点E的直线m与点P的轨迹交于相异两点A．B，设向量
FA
与
FB
夹角为θ，且
3π
4
≤θ＜π，求直线m斜率的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网