题目内容
已知 ,若对任意的非负实数a,b,c,f(a),f(b),f(c)为三角形三边,则k的取值范围是________.
,若对任意的非负实数a,b,c,f(a),f(b),f(c)为三角形三边,则k的取值范围是________.
- <k<4
<k<4
分析:利用三角形三边的性质,得f(a)+f(b)>f(c),通过分类讨论求得到三边之间的关系不等式,解出不等式的解集即可.
解答:∵x2+x+1>0恒成立,f(a),f(b),f(c)为三角形三边,∴f(x)>0恒成立,即x2+kx+1>0(x≥0)恒成立
x=0时,结论成立;x>0时,-k<x+ ,∵x>0,∴x+
,∵x>0,∴x+ ≥2
≥2
∴-k<2
∴k>-2
f(x)= (x>0)
(x>0)
由k>-2
1°、当k=1时,满足题意;
2°、当k>1时,f(x)∈(1,1+ ],由题意知:1+1>1+
],由题意知:1+1>1+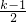 ,∴1<k<4
,∴1<k<4
3°、当k<1时,f(x)∈[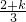 ,1),于是有2×
,1),于是有2×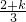 >1,∴1>k>-
>1,∴1>k>-
综上,实数k的取值范围为- <k<4.
<k<4.
故答案为:- <k<4.
<k<4.
点评:此题主要考查不等式的求解方法.
 <k<4
<k<4分析:利用三角形三边的性质,得f(a)+f(b)>f(c),通过分类讨论求得到三边之间的关系不等式,解出不等式的解集即可.
解答:∵x2+x+1>0恒成立,f(a),f(b),f(c)为三角形三边,∴f(x)>0恒成立,即x2+kx+1>0(x≥0)恒成立
x=0时,结论成立;x>0时,-k<x+
 ,∵x>0,∴x+
,∵x>0,∴x+ ≥2
≥2∴-k<2
∴k>-2
f(x)=
 (x>0)
(x>0)由k>-2
1°、当k=1时,满足题意;
2°、当k>1时,f(x)∈(1,1+
 ],由题意知:1+1>1+
],由题意知:1+1>1+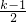 ,∴1<k<4
,∴1<k<43°、当k<1时,f(x)∈[
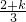 ,1),于是有2×
,1),于是有2×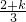 >1,∴1>k>-
>1,∴1>k>-
综上,实数k的取值范围为-
 <k<4.
<k<4.故答案为:-
 <k<4.
<k<4.点评:此题主要考查不等式的求解方法.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
 是定义在
是定义在 上的非负可导函数,且满足
上的非负可导函数,且满足 ,对任意正数
,对任意正数 ,若
,若 ,则必有( )
,则必有( ) B.
B.
 D.
D.
 是定义在
是定义在 上的非负可导函数,且满足
上的非负可导函数,且满足 .对任意正数
.对任意正数 ,若
,若 ,则必有( )
,则必有( ) B.
B.
 D.
D.
 是定义在
是定义在 上的非负可导函数,且满足
上的非负可导函数,且满足 ,对任意正数
,对任意正数 ,若
,若 ,则
,则 的大小关系为
的大小关系为  B.
B.
 D.
D.