Question

已知数列{a_n}各项均为正数，其前n项和为S_n，且满足4S_n=(a_n+1)².

(1)求{a_n}的通项公式；

(2)设b_n=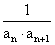，数列{b_n}的前n项和为T_n,求T_n的最小值；

Answer 1

 (1)因为(a_n+1)²=4S_n,所以S_n=,S_n+1=.

所以S_n+1-S_n=a_n+1=

即4a_n+1=a_n+1²-a_n²+2a_n+1-2a_n,

∴2(a_n+1+a_n)=(a_n+1+a_n)(a_n+1-a_n).

因为a_n+1+a_n≠0,所以a_n+1-a_n=2,即{a_n}为公差等于2的等差数列.由(a₁+1)²=4a₁,解得a₁=1,所以a_n=2n-1.

(2)由(1)知b_n==,

∴T_n=b₁+b₂+…+b_n

=

∵T_n+1-T_n=

∴T_n+1>T_n.∴数列{T_n}为递增数列，

∴T_n的最小值为T₁=.