题目内容
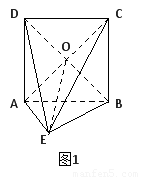
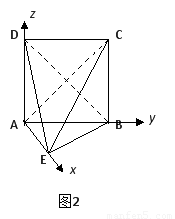
在如图所示的几何体中,四边形ABCD为正方形,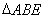 为等腰直角三角形,
为等腰直角三角形,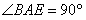 ,且
,且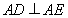 .
.
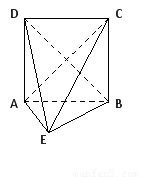
(1)证明:平面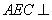 平面
平面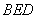 .
.
(2)求直线EC与平面BED所成角的正弦值.
(1)详见解析;(2)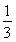 .
.
【解析】
试题分析:解法一利用综合法证明解题:
(1)由已知可知AE⊥AB,又AE⊥AD,所以AE⊥平面ABCD,所以AE⊥DB,又ABCD为正方形,所以DB⊥AC,所以DB⊥平面AEC,而BD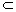 平面BED,故有平面AEC⊥平面BED.
平面BED,故有平面AEC⊥平面BED.
(2)如图4-1中,设AC与BD交点为O,所以OE为两平面AEC和BED的交线.过C作平面BED的垂线,其垂足必在直线EO上,即∠OEC为EC与平面BED所成的角.再设正方形边长为2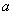 ,则OA=
,则OA=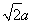 ,AE=2
,AE=2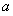 ,所以OE=
,所以OE=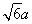 ,EC=
,EC=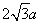 ,所以在三角形OEC中,利用余弦定理可得 cos∠OEC=
,所以在三角形OEC中,利用余弦定理可得 cos∠OEC=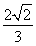 ,故所求为sin∠OEC=
,故所求为sin∠OEC=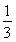 .
.
解法二利用向量法:以A为原点,AE、AB、AD分别为x,y,z轴建立空间直角坐标系,如图4-2所示,
(1)设正方形边长为2,则E(2,0,0),B(0,2,0),C(0,2,2),D(0,0,2) 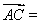 (0,2,2),
(0,2,2),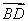 =(0,-2,2),
=(0,-2,2),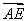 =(2,0,0),
=(2,0,0),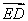 =(-2,0,2),从而有
=(-2,0,2),从而有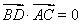 ,
,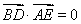 ,即BD⊥AC,BD⊥AE,所以BD⊥平面AEC,故平面BED⊥平面AEC.
,即BD⊥AC,BD⊥AE,所以BD⊥平面AEC,故平面BED⊥平面AEC.
(2)设平面BED的法向量为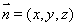 ,由
,由 ,得
,得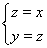 ,故取
,故取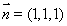 8分
8分
而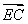 =(-2,2,2),设直线EC与平面BED所成的角为
=(-2,2,2),设直线EC与平面BED所成的角为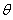 ,则有
,则有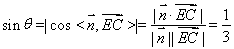 .
.
试题解析:解法一:
(1)由已知有AE⊥AB,又AE⊥AD,
所以AE⊥平面ABCD,所以AE⊥DB, 3分
又ABCD为正方形,所以DB⊥AC, 4分
所以DB⊥平面AEC,而BD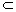 平面BED
平面BED
故有平面AEC⊥平面BED. 6分
(2)设AC与BD交点为O,所以OE为两平面AEC和BED的交线.
过C作平面BED的垂线,其垂足必在直线EO上,
即∠OEC为EC与平面BED所成的角. 7分
设正方形边长为2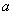 ,则OA=
,则OA=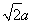 ,AE=2
,AE=2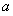 ,
,
所以OE=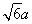 ,EC=
,EC=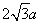 , 9分
, 9分
所以在三角形OEC中,
由余弦定理得 cos∠OEC=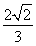 ,故所求为sin∠OEC=
,故所求为sin∠OEC=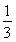 12分
12分
解法二:以A为原点,AE、AB、AD分别为x,y,z轴建立空间直角坐标系. 1分
(1)设正方形边长为2,则E(2,0,0),B(0,2,0),C(0,2,2),D(0,0,2) 2分
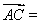 (0,2,2),
(0,2,2),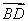 =(0,-2,2),
=(0,-2,2),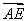 =(2,0,0),
=(2,0,0),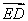 =(-2,0,2),
=(-2,0,2),
从而有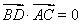 ,
,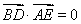 ,
,
即BD⊥AC,BD⊥AE,
所以BD⊥平面AEC,
故平面BED⊥平面AEC. 6分
(2)设平面BED的法向量为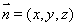 ,
,
由 ,得
,得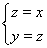 ,故取
,故取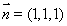 8分
8分
而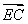 =(-2,2,2),设直线EC与平面BED所成的角为
=(-2,2,2),设直线EC与平面BED所成的角为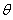 ,
,
则有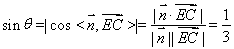 12分
12分
考点:1.直线与平面垂直的判定定理,平面与平面垂直的判定定理;2.直线与平面成角.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案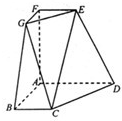 在如图所示的几何体中,四边形ABCD、ADEF、ABGF均为全等的直角梯形,且BC∥AD,AB=AD=2BC.
在如图所示的几何体中,四边形ABCD、ADEF、ABGF均为全等的直角梯形,且BC∥AD,AB=AD=2BC.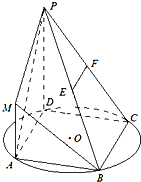 在如图所示的几何体中,平行四边形ABCD的顶点都在以AC为直径的圆O上,AD=CD=DP=a,AP=CP=
在如图所示的几何体中,平行四边形ABCD的顶点都在以AC为直径的圆O上,AD=CD=DP=a,AP=CP= (2012•朝阳区一模)在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EF=1,
(2012•朝阳区一模)在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EF=1, 在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.
在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.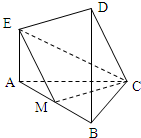 在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,AC=BC=BD=2AE=2,M是AB的中点.
在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,AC=BC=BD=2AE=2,M是AB的中点.