题目内容
如图,直三棱柱ABC-A1B1C1中,AB=BC,∠ABC=120°,Q是AC上的点,AB1∥平面BC1Q.
(Ⅰ)确定点Q在AC上的位置;
(Ⅱ)若QC1与平面BB1C1C所成角的正弦值为
,求二面角Q-BC1-C的余弦值.
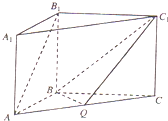
(Ⅰ)确定点Q在AC上的位置;
(Ⅱ)若QC1与平面BB1C1C所成角的正弦值为
| ||
| 4 |

(Ⅰ)连接B1C交BC1于点P,连接PQ.
因为直线AB1∥平面BC1Q,AB1?平面AB1C,平面BC1Q∩平面AB1C=PQ,
所以AB1∥PQ.
因为P为B1C的中点,且AB1∥PQ,
所以,Q为AC的中点.
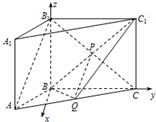
(II)如图建立空间直角坐标系,设AB=BC=a,BB1=b,则平面BC1C的法向量
=(1,0,0).
B(0,0,0),C1(0,a,b),Q(
a,
a,0),
∴
=(0,a,b),
=(-
a,
a,b).
∵QC1与平面BC1C所成角的正弦值为
,
∴
=|cos<
,
>|=
=
,化为3a2=4b2,取b=
a.
设平面C1BQ的法向量为
=(x,y,z),则
,即
,及b=
a.
令x=1,解得y=-
,z=2,∴
=(1,-
,2).
∴cos<
,
>=
=
=
.
故二面角Q-BC1-C的余弦值为
.
因为直线AB1∥平面BC1Q,AB1?平面AB1C,平面BC1Q∩平面AB1C=PQ,
所以AB1∥PQ.
因为P为B1C的中点,且AB1∥PQ,
所以,Q为AC的中点.
(II)如图建立空间直角坐标系,设AB=BC=a,BB1=b,则平面BC1C的法向量
| m |
B(0,0,0),C1(0,a,b),Q(
| ||
| 4 |
| 1 |
| 4 |
∴
| BC1 |
| QC1 |
| ||
| 4 |
| 3 |
| 4 |
∵QC1与平面BC1C所成角的正弦值为
| ||
| 4 |
∴
| ||
| 4 |
| QC1 |
| m |
|
| ||||
|
|
| ||||||
|
| ||
| 2 |
设平面C1BQ的法向量为
| n |
|
|
| ||
| 2 |
令x=1,解得y=-
| 3 |
| n |
| 3 |
∴cos<
| m |
| n |
| ||||
|
|
| 1 | ||
|
| ||
| 4 |
故二面角Q-BC1-C的余弦值为
| ||
| 4 |


练习册系列答案
相关题目
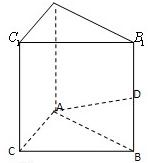
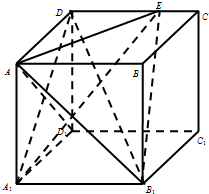
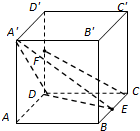
 中,
中,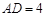 ,
,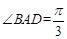 ,
,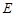 为
为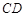 中点,若
中点,若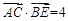 ,则
,则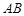 的长为
的长为