Question

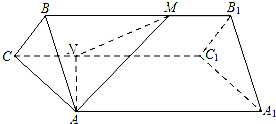（2013•徐州三模）如图，在正三棱柱ABC-A₁B₁C₁中，已知AA₁=6，AB=2，M，N分别是棱BB₁，CC₁上的点，且BM=4，CN=2．
（1）求异面直线AM与A₁C₁所成角的余弦值；
（2）求二面角M-AN-A₁的正弦值．

Answer 1

分析：（1）通过建立空间直角坐标系，利用异面直线的方向向量的夹角即可得到；
（2）求出二面角的两个平面的法向量的夹角即可．

解答：解：（1）以AC的中点为原点O，分别以OA，OB所在直线为x，z轴，建立空间直角坐标系O-xyz（如图）．
则O（0，0，0），A（1，0，0），C（-1，0，0），B(0，0，

3

)，
N（-1，2，0），M(0，4，

3

)，A₁（1，6，0），C₁（-1，6，0）．
∴

AM

=(-1，4，

3

)，

A1C1

=(-2，0，0)．
∴cos＜

AM

，

A1C1

＞=

AM • A1C1

| AM || A1C1 |

=

2

2 20

=

5

10

，
所以异面直线AM与A₁C₁所成角的余弦值为

5

10

．
（2）平面ANA₁的一个法向量为

m

=（0，0，1）．
设平面AMN的法向量为

n

=（x，y，z），因为

AM

=(-1，4，

3

)，

AN

=(-2，2，0)，
由

n • AM =0 n • AN =0

得

-x+4y+ 3 z=0 -2x+2y=0

令x=1，则y=1，z=-

3

．
∴

n

=(1，1，-

3

)．
∴cos＜

m

，

n

＞=

m • n

| m | | n |

=

- 3

5

=-

15

5

，
所以二面角M-AN-A₁的正弦值=

1-(- 15 5 )2

=

10

5

．

点评：熟练掌握通过建立空间直角坐标系并利用异面直线的方向向量的夹角求出异面直线的夹角、二面角的两个平面的法向量的夹角得到二面角的平面角的方法是解题的关键．