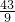Question

已知A（2，2，1），B（-1，3，4），C（1，1，4），

AP

=2

PB

，则|

PC

|为（　　）

• A．

  43

  3

• B．

  43

  9

• C．

  43

  3

• D．

  43

  9

Answer 1

分析：设P（x，y，z），由A（2，2，1），B（-1，3，4，）利用

AP

=2

PB

，求出可得P，由两点间的距离公式可求PC．

解答：解：设P（x，y，z）
∵A（2，2，1），B（-1，3，4，）
∴

AP

=（x-2，y-2，z-1），

PB

=（-1-x，3-y，4-z）
∵

AP

=2

PB

，x-2=-2-2x，解得x=0，y-2=6-2y，解得y=

8

3

，z-1=8-2z，解得z=3
∴P（0，

8

3

，3），C（1，1，4），
则|PC|=

(1-0 )2+(1- 8 3  )2+(3-4)2

=

43

3

．
故选A．

点评：本题主要考查了向量共线的坐标表示，两点间的距离公式的应用，考查计算能力．